Scroll to:
Prediction of the concentration inhomogeneity of powder magnetic hard alloys based on the Fe-Cr-Co-Mo system and the effect of Sm additions on their magnetic properties
https://doi.org/10.17073/1997-308X-2023-1-12-20
Abstract
Hysteresis alloys based on Fe-Cr-Co system are extensively used in the instrument-making industry as a material for synchronous motors of navigation systems, in the electronic industry, and other mechanical engineering fields. The following requirements are imposed on Fe-Cr-Co alloys: temperature stability of magnetic characteristics over time, manufacturability, low porosity and concentration inhomogeneity, which allow to obtain high-quality magnetic and mechanical properties. Materials based on conventional alloying systems, such as Fe-Cr-Co, have outlived themselves. An urgent line of the development of new materials and improvement of the properties of existing ones is alloying with rare-earth metals. The effect produced by Sm addition on powder analogs of Fe-Cr-Co system remains unstudied. In this paper, 22Kh15K4MS powder magnetic hard alloy alloyed with samarium in an amount of 0.5 wt. % was studied. The billets were obtained by cold pressing at a pressure of 600 MPa followed by vacuum sintering. The concentration inhomogeneity of Cr, Co, Mo, Sm was determined after 12 different sintering modes. A model of diffusion homogenization of ridge alloys, which allows to numerically evaluate the effect of sintering modes on the concentration inhomogeneity, was plotted. The distributions of chromium, cobalt, and molybdenum correspond to the asymptotically logarithmically normal law. Samarium is unevenly distributed in the structure. The effect of samarium additions on the magnetic properties of the alloy has been demonstrated. The alloying of 22Kh15K4MS alloy with 0.5 wt. % of samarium allows to obtain powder hysteresis magnets with a coercive force in the range from 3.9 to 33.0 kA/m and a residual magnetic induction from 0.44 to 0.95 T.
Keywords
For citations:
Marieva M.A., Shatsov A.A. Prediction of the concentration inhomogeneity of powder magnetic hard alloys based on the Fe-Cr-Co-Mo system and the effect of Sm additions on their magnetic properties. Powder Metallurgy аnd Functional Coatings (Izvestiya Vuzov. Poroshkovaya Metallurgiya i Funktsional'nye Pokrytiya). 2023;17(1):12-20. https://doi.org/10.17073/1997-308X-2023-1-12-20
Introduction
In order to obtain materials with specified characteristics, it is necessary to establish the relationship between structure and properties [1]. Porosity and concentration inhomogeneity have a considerable effect on the processes of structure formation and magnetic properties of alloys [2–4], reducing their mechanical, physical and performance characteristics [5]. The inhomogeneity of alloys is estimated using diffusion coefficients [6–8], however, their determination does not allow to predict the concentration inhomogeneity with reasonable accuracy, since it is associated not only with diffusion, but also depends on a number of other factors [9; 10]. The study of diffusion at the stage of sintering of powder materials is performed using diffusion couples, however, the application of this method within multicomponent systems results in considerable experimental difficulties [11; 12]. The numerical methods for solving homogenization equations [13–15] do not take into account the properties of powder particles, their shape and defectiveness, and models based on statistical processing of data on diffusion homogenization provide only qualitative information on the element distribution. One of the modern approaches to the study of diffusion is the experimental study of homogenization patterns [13].
In work [16], the non-monotonic effect of concentration inhomogeneity on the magnetic properties of a material was proved experimentally. Furthermore, there is an approach based on the assertion that the homogenization process has a noticeable effect on the properties due to a change in the phase composition and distribution of phases, and a parallel transformation of the porous structure. In this paper, such a statistical value as concentration variation coefficient (V) was taken as a criterion for the inhomogeneity of the alloying element distribution. The technique allows to determine and predict the inhomogeneity and distribution of elements, provides a criterion for comparing the homogeneity of powder steels and alloys, allows to select the composition of materials and the technology for their production. The validity of this method for assessing inhomogeneity has been repeatedly confirmed in works [1; 11].
Recently, the alloys based on Fe–Cr–Co system with alloying additions, including rare-earth metals, have been extensively studied. The ferromagnetic materials based on SmCo5 , Sm2Co17 compounds are widely used for the production of permanent magnets [17]. They exhibit a high Curie temperature, anisotropy field, and remanence, but exhibit high hardness and poor processibility. The alloys of Fe–Cr–Co system exhibit a high temperature stability, corrosion resistance, ductility and lower production costs compared to hard magnets made of rare-earth metals. In work [18], the alloying of a cast alloy of Fe–Cr–Co system with samarium up to 2 wt. % resulted in a significant increase in its magnetic properties: BHmax by 86 %, Br by 47 %, and Hc by 28.7 %. The described approach to the alloying of chromel-copel alloys is of scientific and practical interest, however, the impact of concentration inhomogeneity on the effect of samarium additions has not been studied.
The study is aimed at the development of a homogenization model for predicting the modes of sintering of concentration-inhomogeneous powder hard magnetic alloys based on Fe–Cr–Co system with samarium.
Research methodology
This paper investigates the samarium-alloyed 22Kh15K4MS powder alloy, which exhibits the following chemical composition, wt. %:
| Fe | Cr | Co | Mo | Si | Sm |
| 57.0 | 22.5 | 15.0 | 4.0 | 1.0 | 0.5 |
The following powders of metals and alloys were used as initial components of the charge: chromium PKh-1S (TU 14-5-298-99, average particle size r = 10 µm, standard deviation σ = 5 µm); cobalt GP-OK (TU 1793-008-92, r = 24 µm, σ = 13 µm); iron OSCh 6-2 (TU 6-09-05808008-262-92, r = 2 µm, σ = 2 µm); ferrosilicon FS50 (GOST 1415-93-92, r = 8 µm, σ = 4 µm); molybdenum MPCh (TU 48-19-69-80, r = 2 µm, σ = 1 µm); samarium-cobalt (GOST 21559-76, r = 39 µm, σ = 21 µm).
The charge was sieved through a mesh with a cell size of 63 μm and averaged in a mixer with a shifted rotation axis for 8 h.
The sample billets were obtained by cold pressing at a pressure of 600 MPa, followed by vacuum sintering with a residual pressure of 10–2 Pa according to the modes specified in Table 1.
Table 1. The sintering modes of 22Kh15K4MS alloy
|
The sintering temperature range was selected on the basis of the fact that sintering at temperatures below 1200 °C results in obtaining magnets with a non-magnetic γ-phase production. Increasing the sintering temperature up to 1400 °C causes the evaporation of components from the surface of the billets. In both cases, these processes lead to the deterioration of the magnetic properties of the alloy [19].
All samples were quenched in 15 % aqueous NaCl solution at the temperature starting from 1250 °C. The aging of the billets was performed sequentially at 9 stages, and the processing indices are provided in Table 2. The main parameters and the shape of the magnetic hysteresis loop of the test samples were determined by means of “Permagraph L” hysteresis graph (Magnet-Physik, Germany) with PERMA software after the quenching and multistage aging.
Table 2. Billet aging modes
|
To examine the patterns of changes in the concentration inhomogeneity of element distribution during sintering, the concentrations of Cr, Co, Mo, and Sm were measured at 100 points being equidistant from each other on the surface of the section. The concentrations were measured by the method of X-ray microanalysis, using “Tescan Mira 3” electron microscope (Tescan, Czech Republic). The measure of concentration inhomogeneity is the relative fluctuation of concentration, i.e. the concentration variation coefficient V, being equal to the ratio of the square root of the concentration dispersion to its average value:
| \[V = \frac{{\sqrt D }}{C},\] | (1) |
where D is the element concentration dispersion, and С is the average concentration [16].
The assumption of the logarithmic normality of the distributions was tested using Pearson’s χ2 test. The entire measurement range of the random variable was divided into disjoint intervals k. In accordance with the given division, the number of sample values that fell within the i-th interval (designated as ni ). The obtained histogram of the sampling distribution serves as the basis for selecting the distribution law [20]. The value characterizing the deviation of the sample distribution from the predicted one is determined by the following formula:
| \[{\chi ^2} = \frac{{{{({n_i} - n{p_i})}^2}}}{{n{p_i}}},\] | (2) |
where n is the sample volume; ni is the number of sample elements, falling within the i-th interval; pi is the probability that the random variable under study falls into the i-th interval, calculated in accordance with the hypothetical distribution law F(x).
In order to predict the concentration inhomogeneity, the following homogenization equation was used:
| \[{V_j} = {\alpha _j}\exp \left( {{\beta _j}tc_j^{2/3}\exp \left[ { - \frac{{{Q_j}}}{{RT}}} \right]} \right),\] | (3) |
where Vj and cj are the variation coefficient and the average concentration of the j-th matrix component; t (h) and T (K) are the sintering time and temperature, respectively; R is the gas constant, J/(mol·K); Qj is the effective activation energy of mutual diffusion in the system, J/(mol·K); αj and βj are the coefficients [16].
Research result and disussion
The structure of the alloys after quenching represented an α-solid solution of Cr, Co, Mo, and Si. Samarium was in the form of individual inclusions (Fig. 1) with very low solubility in the α-phase. The presence of dark areas in Fig. 1 testifies to the residual porosity of the material.
Fig. 1. The microstructure of 22Kh15K4MS alloy |
The first stage was to obtain the values of the concentration inhomogeneity for Cr, Co, Mo, Sm. The concentration inhomogeneity decreased with an increase in the sintering temperature and holding time (Table 3).
Table 3. Experimental (numerator) and predicted (denominator)
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
To determine the law of distribution of concentrations, Pearson’s χ2 criterion was calculated after each of 12 sintering modes. No distributions corresponding to the normal law were identified for chromium. 7 distributions out of 12 distributions corresponded to the logarithmically normal law. A similar pattern was observed when calculating χ2 for cobalt and molybdenum. Samarium is unevenly distributed in the structure, so it is impossible to establish the law of its distribution within the specified scope of the experiment.
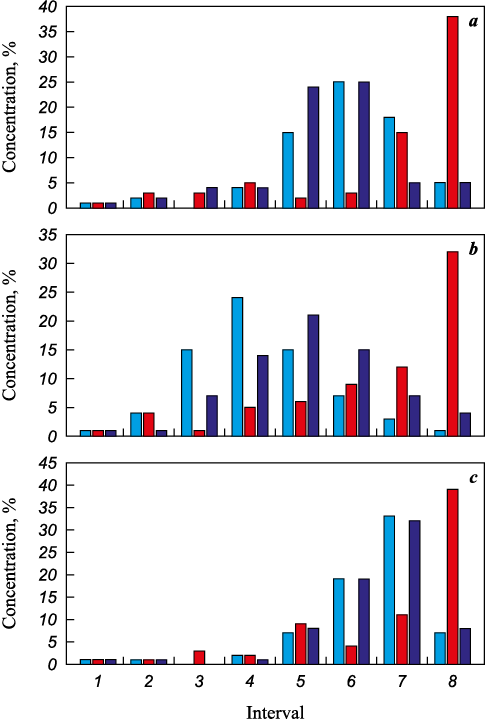
Upon the construction of element distribution histograms, the entire range of data was divided into 8 intervals (Fig. 2). The distribution histograms of chromium, cobalt, and molybdenum exhibited a right-hand asymmetry, which increased with rising temperature and sintering time.
Fig. 2. Distribution histograms of cobalt concentrations (а), |
The approximation of experimental data (Table 3, numerator) allowed to determine αj , βj coefficients of the homogenization equation, activation energy Q (Table 4), as well as the predicted values V (Table 3, denominator). Due to the uneven distribution of samarium in the structure and high values of concentration inhomogeneity, the prediction of VSm was not performed.
Table 4. Activation energies and equation coefficients
|
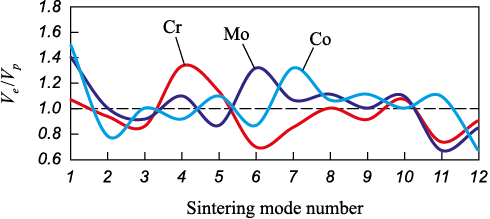
The dependence of Ve ratio (the experimental coefficient of variation) to Vp ratio (predicted) on the sintering mode was plotted (Fig. 3). The closest Ve and Vp ratios were obtained upon modes 4, 6, 8, 9, 10, which correspond to sintering at temperatures of 1300 °C (1 and 8 h), 1350 °C (3 and 8 h), and 1380 °C (1 h).
Fig. 3. The dependence of Ve ratio (experimental) |
QCr values correspond to the activation energy of chromium in the α-Fe phase of the cast alloy obtained in work [21]. The activation energy amounted to 197 ± 10 kJ/(mol·K) for the alloy with 25.8 wt. % of Сr, which is likely associated with the formation of low-soluble compounds during the heating. QCo value appeared to be higher than the one specified in the literary sources [22].
An increase in sintering temperature and sintering time resulted in an increase in homogeneity and a decrease in V coefficient. Activation energy QMo appeared to be at the level of activation energy in binary alloys of iron with Mo [20], which is associated with a high ratio of surfaces and the formation of low-soluble compounds during the heating. In Fe–6%Mo alloy, the activation energy is at the level of 262.5 J/(mol·K), and in powder alloy QMo it accounts for 282 J/(mol·K) (Table 4).
Sintering at 1250 °C allows to obtain V at the level of 0.16–0.12 for Cr, 0.3–0.1 for Co, at the level of 0.5–0.2 for Mo, and at the level of 0.9–1.1 for Sm, depending on the sintering time. It is noted that the resulting concentration inhomogeneity is directly proportional to the atomic mass of the element. An increase in the sintering temperature up to 1300 °C results in V decrease only after 8 h of holding: 0.09 for Cr and 0.11 for Co, the inhomogeneity values remain the same for Mo. The lowest values of concentration inhomogeneity were obtained after sintering at 1380 °C for 8 h: 0.09 for Cr, 0.06 for Co, and 0.16 for Mo. A further increase in the sintering temperature requires more energy and may result in intense evaporation of chromium from the surface of the billets, which, in turn, will lead to inhomogeneity of the chemical composition between the surface layer and the volume of the sample and a decrease in magnetic properties [5; 23]. Thus, for powder magnets made of 22Kh15K4MS alloy, alloyed with Sm, the optimal sintering mode is the one at a temperature of 1350 °C for 1–3 h. The concentration inhomogeneity of Cr, Co, and Mo, depending on the holding time, varies within 0.01–0.06 (Table 3). The application of quenching after sintering allows to reduce the concentration inhomogeneity of chromium and cobalt to the level of V = 0.06 ÷ 0.08 [24].
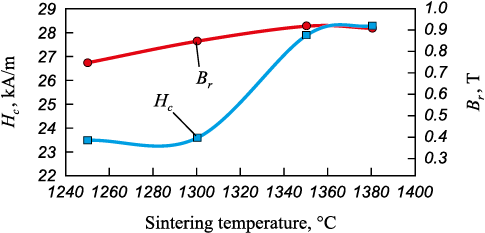
The magnetic properties of the samples after sintering for 8 h, quenching, and multistage aging (see Table 2) at various sintering temperatures (Fig. 4) were determined. Upon an increase in sintering temperature from 1250 to 1380 °C, an increase in the level of magnetic properties by 18–20 % was observed, which is associated with a decrease in the concentration inhomogeneity of the alloy (Table 3). The optimum magnetic properties were also obtained after sintering at 1350 °C.
Fig. 4. The dependence of coercive force (Hc ) |
For testing the homogenization model as per equation (3), the sintering time for each mode and element was calculated. Table 5 shows the calculated sintering time for the element with the longest homogenization time at a given temperature. According to the results obtained, the level of concentration inhomogeneity is achieved in a shorter time at temperatures of 1250 and 1300 °С (1, 3 and 8 h), 1350 °С (1–3 h), 1380 °С (1 h). At sintering temperatures of 1350 °C, 1380 °C and holding time of 3–8 h, the calculated sintering time significantly exceeds the actual time. This is associated with the fact that the activation energy may not match the value used in the calculation. The used effective activation energy is applicable precisely for this process at the boundary of the existing model.
Table 5. Calculated sintering times
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
To assess the effect of samarium addition on the magnetic properties of 22Kh15K4MS alloy, the multistage aging of samples without samarium as well as samples with 0.5 wt. % of Sm was performed. The fastest growth of the magnetic properties (Br and Hc ) of the alloy with 0.5 wt. % of Sm occurred at the first three stages of aging. In subsequent stages, only Hc growth continued. Upon that, the magnetic induction Br reached its peak at the 4th stage of aging with further permanent decrease (Table 6).
Table 6. Magnetic properties of the 22Kh15K4MS alloy
| ||||||||||||||||||||||||
The rectangularity coefficient of magnetic hysteresis loop (Cr ) had the highest value after the 3rd stage of aging (Table 6). Compared to the initial alloy, Cr is 9–11 % higher for the alloyed alloy under this heat treatment mode. According to the X-ray diffraction analysis performed in work [25], the diffraction peaks corresponding to Sm2Co17 (64.9°, 74.68°) and SmCo5 (50.798°) phases were identified in the samples after aging, except for the α-phase. This, in turn, testifies to the redistribution of samarium during aging and the production of a stoichiometric composition distinct from the initial component.
Conclusions
1. The distributions of chromium, cobalt, and molybdenum correspond to the asymptotically logarithmically normal law. Samarium is unevenly distributed in the structure, therefore, it is impossible to establish the law of its distribution within the specified scope of the experiment. The homogenization process did not effect the homogeneity of samarium distribution, which is apparently associated with the non-solubility of Sm in iron.
2. A complete statistical description of the distribution of Cr, Co, Mo of 22Kh15K4MS ridge alloy with the addition of samarium in the amount of 0.5 wt. % is presented. Based on the experimental determination of V criterion, a homogenization equation, which allows to numerically evaluate the effect of sintering modes on the concentration inhomogeneity, was obtained.
3. The optimal sintering mode for powder magnets made of samarium-alloyed 22Kh15K4MS alloy was experimentally selected.
4. The alloying of 22Kh15K4MS alloy with samarium in an amount of 0.5 wt. % makes it possible to obtain powder hysteresis magnets with a coercive force of 3.9–33.0 kA/m and a residual magnetic induction of 0.44–0.95 T at Cr up to 0.73, which constitutes an actual index for precision tool-making.
References
1. Анциферов В.Н., Беклемышев А.М., Гилев В.Г., Порозова С.Е., Швейкин Г.П. Проблемы порошкового материаловедения. Часть 2: Высокопористые проницаемые материалы. Екатеринбург: УрО РАН, 2002. 261 с.
2. Yamashita M., Fujimura S. Sintered Fe-Cr-Co type magnetic alloy and method for producing article made thereof: Pat. 4601876 (USA). 1986.
3. Ternero F., Rosa L.G., Urban P., Montes J.M., Cuevas F.G. Influence of the total porosity on the properties of sintered materials - A review. Metals. 2021;11(5):730. https://doi.org/10.3390/met11050730
4. Bocchini G.F. The influences of porosity on the characteristics of sintered materials. International Journal of Powder Metallurgy (Princeton, New Jersey). 1986;07: 185-186, 188. https://doi.org/10.4271/860148
5. Ustyuhin A.S., Alymov M.I., Milyaev I.M. Magnetic hysteresis properties of Fe-26Cr-16Co hard magnetic alloys. Letters on Materials. 2014;4(1):59-61. (In Russ.). https://doi.org/10.22226/2410-3535-2014-1-59-61
6. Zhang B. Calculation of self-diffusion coefficients in iron. AIP Advances. 2014;4(1):017128. https://doi.org/10.1063/1.4863462
7. Xiao Y.Z., Ji-Hua Z., Yuan W., Xu-Sheng Y., Turab L., Hong-Hui W. Machine learning assisted design of FeCoNiCrMn high-entropy alloys with ultra-low hydrogen diffusion coefficients. Acta Materialia. 2022; 224:117535. https://doi.org/10.1016/j.actamat.2021.117535
8. Serin B., Ellickson R.T. Determination of diffusion coefficients. Journal of Chemical Physics. 1941;(9):742-747.
9. Balogh J., Kemeny T., Vincze I., Bujdoso L., Toth L., Vincze G. Amorphous alloy formation by mechanical alloying and consecutive heat treatment in Fe50B50 powder mixture. Journal of Applied Physics. 1995;77(10): 4997-5003. https://doi.org/10.1063/1.359522
10. Ivasishin O.M., Eylon D., Bondarchuk V.I., Savvakin D.G. Diffusion during powder metallurgy synthesis of titanium alloys. Defect and Diffusion Forum. 2008;277:177-185. https://doi.org/10.4028/www.scientific.net/DDF.277.177
11. Dash A., Paul A. Body diagonal diffusion couple method for estimation of tracer diffusion coefficients in a multi-principal element alloy. https://doi.org/10.48550/arXiv.2205.06550 (accessed: 25.11.2022).
12. Purdy G.R., Kirkaldy J.S. Homogenization by diffusion. Metallurgical Transactions. 1971;2(2):371-378. https://doi.org/10.1007/BF02663324
13. Анциферов В.Н., Пещеренко С.Н., Курилов П.Г. Взаимная диффузия и гомогенизация в порошковых материалах. М.: Металлургия, 1988. 152 с.
14. Bulanov V.Ya., Krashaninin V.A., Oglezneva S.A. Modeling of homogenization of binary powder alloys. Konstruktsii iz kompozitsionnykh materialov. 2006;(4): 181-187. (In Russ.).
15. Engquist B., Souganidis P.E. Asymptotic and numerical homogenization. Acta Numerica. 2008;(17):147-190. https://doi.org/10.1017/S0962492906360011
16. Ryaposov I.V., Kleiner L.M., Shatsov A.A. Concentrationprecision non-uniform soft-magnetic alloys based on the system Fe-Si-Al. Vestnik Permskogo natsional'nogo issle-dovatel'skogo politekhnicheskogo universiteta. Mashi no-stroenie, materialovedenie. 2011;13(3):92-102. (In Russ.).
17. Ormerod J. Powder metallurgy of rare earth permanent magnets. The International Journal of Powder Metallurgy. 1989;25(3):197-205.
18. Tao S., Ahmad Z., Zhang P., Zheng X., Zhang S. Effects of Sm on structural, textural and magnetic properties of Fe-28Cr-20Co-3Mo-2V-2Ti hard magnetic alloy. Journal of Alloys and Compounds. 2020;816:152619. https://doi.org/10.1016/j.jallcom.2019.152619
19. Ustyukhin A., Alymov M., Ashmarin A., Milyaev I., Zelenskii V., Ankudinov A. The phase composition of powder hard magnetic Fe-30Cr-(8-24)Co alloys sintered under different temperature conditions. Doklady Akademii Nauk. 2018;482(2):172-176. (In Russ.). https://doi.org/10.31857/S086956520003475-5
20. Ахназарова С.Л., Кафаров В.В. Оптимизация эксперимента в химии и химической технологии. М.: Высшая школа, 1978. 319 с.
21. Блантер М.Е. Теория термической обработки. Учебник для вузов. М.: Металлургия, 1984. 328 с.
22. Павлинов Л.В. Диффузия в двойных и многокомпонентных сплавах на основе железа в области а- и Y-твердых растворов. Обнинск: Физико-энергетический институт, 1976. 38 c.
23. Ustyukhin A.S., Ankudinov A.B., Zelenskii V.A., Mi-lyaev I.M., Alymov M.I. Improvement of magnetic properties by hot rolling of sintered powder alloy in the Fe-Cr-Co system. Doklady Physical Chemistry. 2017;476(2):193-196. https://doi.org/10.1134/S0012501617100074
24. Marieva M.A., Shatsov A.A. Control of hysteretic properties in powder alloys based on the Fe-Cr-Co system. Powder Metallurgy and Functional Coatings. 2021; 15(3):14-21. (In Russ.). https://doi.org/10.17073/1997-308X-2021-3-14-21
25. Marieva M.A., Kozvonin V.A., Shatsov A.A. Increasing the rectangularity of the loop of magnetic hysteresis of magnetic hysteresis based on the Fe-Cr-Co system due to the alloying Sm. Bulletin PNRPU. Mechanical engineering, materials science. 2021;23(3):39-46. (In Russ.).
About the Authors
M. A. MarievaRussian Federation
Marya A. Marieva - Postgraduate Student of the Department of metal science, thermal and laser processing of metals.
29 Komsomolskiy Prosp., Perm 614990
A. A. Shatsov
Russian Federation
Alexandr A. Shatsov - Dr. Sci. (Eng.), Prof. of the Department of metal science, thermal and laser processing of metals.
29 Komsomolskiy Prosp., Perm 614990
Review
For citations:
Marieva M.A., Shatsov A.A. Prediction of the concentration inhomogeneity of powder magnetic hard alloys based on the Fe-Cr-Co-Mo system and the effect of Sm additions on their magnetic properties. Powder Metallurgy аnd Functional Coatings (Izvestiya Vuzov. Poroshkovaya Metallurgiya i Funktsional'nye Pokrytiya). 2023;17(1):12-20. https://doi.org/10.17073/1997-308X-2023-1-12-20
JATS XML