Перейти к:
Роль примесей в изменении фазового состава в системе Al–Fe–C при спекании
https://doi.org/10.17073/1997-308X-2023-2-5-13
Аннотация
Эффективное использование материальных ресурсов заставляет активнее обращать внимание на отходы производства с целью не только простой их утилизации, но и их использования в качестве источника некоторых элементов и как компонентов порошковых материалов. Стальная стружка – сложный многокомпонентный материал на основе железа. Наличие примеси, например углерода, может оказывать влияние на диффузионное взаимодействие смеси стружки с порошком другого металла. В данной работе рассмотрен один из возможных вариантов диффузионного взаимодействия алюминия и стальной стружки в условиях вакуумного спекания с регулируемым нагревом. После спекания был проведен микроанализ структуры и определен фазовый состав продуктов взаимодействия. Выявлено, что в процессе спекания формируется многофазная структура, в которой не менее 30 % объема занимает алюминид железа FeAl. Несмотря на достаточно высокие температуры, фиксируются остатки алюминия и железа. Среди причин неполного превращения могут быть тугоплавкие продукты взаимодействия, тормозящие диффузию, а также примеси, влияющие на величину и направленность диффузионных потоков. Для подтверждения важной роли примесей в кинетике диффузионного взаимодействия рассмотрены модельные задачи роста интерметаллидной фазы между частицей плоской или сферической формы с окружающим ее алюминием. Учитывается появление перекрестных диффузионных потоков в области растущей фазы и, возможно, влияние примеси на концентрационный предел существования новой фазы. Найдены приближенные аналитические решения, которые позволяют проанализировать динамику роста области, занимаемой растущей фазой, в зависимости от параметров модели.
Ключевые слова
Для цитирования:
Коростелева Е.Н., Князева А.Г., Анисимова М.А., Николаев И.О. Роль примесей в изменении фазового состава в системе Al–Fe–C при спекании. Известия вузов. Порошковая металлургия и функциональные покрытия. 2023;17(2):5-13. https://doi.org/10.17073/1997-308X-2023-2-5-13
For citation:
Korosteleva E.N., Knyazeva A.G., Anisimova M.A., Nikolaev I.O. The impact of impurities on the Al–Fe–C system phase composition changes during sintering. Powder Metallurgy аnd Functional Coatings (Izvestiya Vuzov. Poroshkovaya Metallurgiya i Funktsional'nye Pokrytiya). 2023;17(2):5-13. https://doi.org/10.17073/1997-308X-2023-2-5-13
Введение
Основу современных материальных ресурсов для металлообработки до сих пор составляют различные стали и сплавы на основе железа как наиболее распространенный и дешевый материал. Существует широкий ряд задач материаловедческого характера, направленных на решение проблем не только замены популярных сплавов на более высокоэффективные новые группы материалов, но и утилизации/воспроизводства уже отработанных изделий, деталей и отходов производства [1–4]. Наибольший объем отходов металлообработки формируется за счет обработки стальных заготовок с формированием металлической стружки [5; 6]. Следует иметь в виду, что стальная стружка – прежде всего сложный многокомпонентный материал на основе железа, а вторым важным компонентом в стали является углерод [7].
В зависимости от марки стали в стружке присутствуют и другие элементы в широком диапазоне концентраций. В частности, простейшие группы сталей (например, сталь 45) могут содержать от 0,42 до 0,5 мас. % углерода. Третьим заметным легирующим компонентом являются марганец (до 0,8 %), а также кремний (до 0,37 %). Согласно стандарту допускается присутствие хрома, меди и никеля (до 0,3 % каждого) и в малых количествах – фосфора и серы (не более 0,035 %). Кроме того, стальная стружка – это продукт высокоскоростного процесса резания металлической заготовки, в результате чего на поверхности стружки формируется активированная высокодефектная структура [8].
Как правило, отходы металлообработки утилизируют в процессе повторной переплавки, а все технологические процессы ее сбора и транспортировки ориентированы на формование в более компактные брикеты с предварительной очисткой от продуктов окисления и взаимодействия с охлаждающей жидкостью (СОЖ) [9]. С другой стороны, можно рассматривать стальную стружку как самостоятельный компонент в порошковой (дисперсной) композиции с другими компонентами-элементами [10]. А поскольку измельченные частицы стальной стружки представляют собой многоэлементный состав, то становится актуальной задача прогнозирования процессов диффузионного взаимодействия стружки и другого компонента композиции в условиях нагрева. Понимание таких процессов будет способствовать развитию технологий получения не только новых материалов, но и способов утилизации металлических отходов.
Цель настоящей работы заключалась в анализе влияния присутствия примесей на диффузионное взаимодействие компонентов в системе Al–Fe–C.
Методика эксперимента
В качестве взаимодействующего компонента для композиции с участием измельченной стальной стружки использован алюминий. Система Al–Fe хорошо изучена и присутствует во многих исследованиях [11–16], где алюминий может выступать как матричный материал, так и в качестве легирующей добавки. Согласно диаграмме состояния Al–Fe [17] алюминий хорошо растворим в α-Fe, образуя широкие области твердых растворов (до 32 ат. %), но его растворимость падает в γ-Fe до 1,285 ат. % при высоких температурах. Железо имеет очень ограниченную растворимость в алюминии, не превышая 0,03 ат. % при эвтектической температуре 654 °С. Система характеризуется образованием 5 стабильных интерметаллидов Fe3Al, FeAl, FeAl2 , Fe2Al5 и FeAl3 , диапазон существования которых варьируется в пределах t = 552÷1170 °С.
В качестве модельного состава рассмотрена композиция из измельченной стальной стружки после обработки заготовки из стали 45 с добавлением порошка алюминия марки ПА-4. Соотношение компонентов в смеси составляло 25 мас. % алюминия и 75 мас. % измельченной стальной стружки стали 45. Термообработку композиции осуществляли в вакуумной печи с регулируемым нагревом до 1000 °С. После спекания был проведен микроанализ структуры и определен фазовый состав порошкового материала с провзаимодействовавшими компонентами.
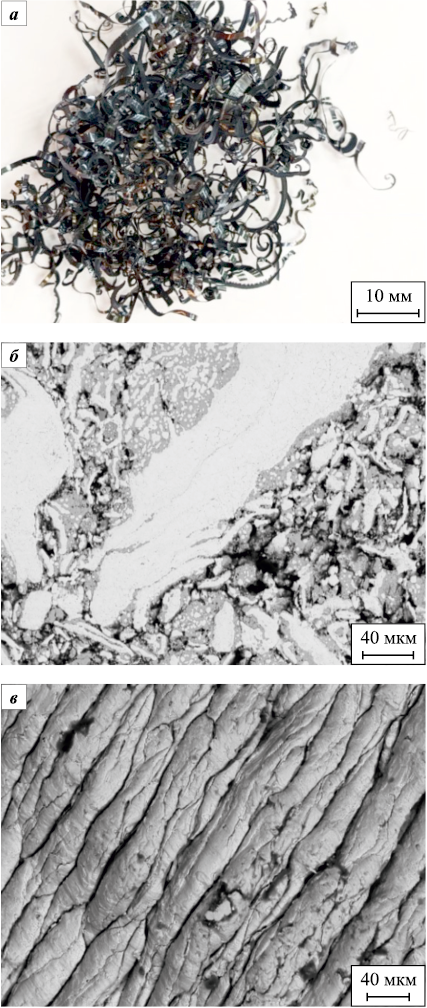
Чтобы дать адекватное представление об особенностях продуктов обработки стальных заготовок (стружки), на рис. 1 приведены общий вид и морфология поверхности фрагмента стальной стружки, а также ее микроструктура после спекания. Анализ содержания углеродной составляющей показал, что концентрация углерода не превышает 1,5 %. Особенности спекания стальной стружки детально исследованы в работе [18].
Рис. 1. Общий вид (а) и морфология поверхности (б) |
При добавлении алюминия к стальной стружке в результате активного процесса сплавообразования с синтезом интерметаллидов формируется многофазная структура (рис. 2), в которой не менее 30 % объема занимает алюминид железа FeAl. Несмотря на достаточно экзотермичный процесс взаимодействия Al и Fe, в продуктах вакуумного спекания порошковой смеси рентгеноструктурный анализ фиксирует остатки Al (не менее 15 об. %) и Fe. То есть реакции взаимодействия алюминия и железа, которое является основой стальной стружки из стали 45, не завершаются в полном объеме даже при температуре спекания 1000 °С, где Al фактически представлен в виде жидкой фазы.
По-видимому, в зоне контакта взаимодействующих частиц, где имеет место диффузионное взаимодействие, присутствуют факторы, влияющие на динамику этих потоков и, как следствие, на полноту и завершенность фазовых превращений. Среди таких факторов могут быть:
Рис. 2. Микроструктура синтезированных порошковых продуктов |
– тугоплавкие продукты взаимодействия, тормозящие диффузию;
– примеси, влияющие на величину и направленность диффузионных потоков;
– дефекты структуры, определяющие особенности диффузии и реакций на микроуровне.
Примеси могут явно не участвовать в образовании новых фаз, но при этом будут оказывать существенное влияние на кинетику фазообразования.
Подтверждением подобных возможностей влияния примесей служит следующая модельная задача.
Математическая модель
Постановка задачи, представленной ниже, основана на том, что основной компонент стальной стружки (железо) – весьма слабо растворим в Al. Растворимость алюминия в железе тоже не очень высока, хотя значение 1,285 % при t = 1150 °С можно принять во внимание (это растворимость при высокой температуре в γ-Fe). Допускается, что каждая фаза обладает некоторой областью гомогенности. Так как один из компонентов смеси является продуктом металлообработки стальных заготовок, то очевидно, что он содержит в качестве примеси углерод, содержание которого с учетом загрязняющих факторов не превышает 1,5 %. Варианты модельной задачи о диффузионном взаимодействии Fe и Al в присутствии третьего компонента основаны на известных фактах изменения путей диффузии и усложнения конкуренции при фазообразовании в системах с числом компонентов больше 2 [19; 20]. Перекрестные диффузионные потоки могут приводить к особенностям в распределении концентраций в разных системах [21–23].
1. В первом варианте модели согласно общему внешнему виду (см. рис. 1, а) рассматриваем стружку как некоторый плоский объект. Алюминий поступает к поверхности железа, что приводит к образованию интерметаллидных фаз. Углерод влияет на диффузию, способствуя появлению перекрестных диффузионных потоков. Формально в произвольный момент времени в каждой фазе могут присутствовать Fe, C и Al. Выделяем только 2 подвижные границы, между которыми расположены всевозможные интерметаллидные фазы (рис. 3). Тогда имеются 3 области, которые соответствуют трем фазам: (Fe + C)–(FexAly)–(Al), разделенным подвижными границами.
Рис. 3. Иллюстрация к математической постановке задачи |
Сумма трех массовых концентраций в каждой фазе равна 1 (в произвольной точке). Поэтому в общем случае нам требуются только 2 диффузионных уравнения для каждой выделенной области:
| \[\frac{{\partial {C_{1,k}}}}{{\partial t}} = \frac{\partial }{{\partial x}}\left( {D_{11}^{(k)}\frac{{\partial {C_{1,k}}}}{{\partial x}}} \right) + \frac{\partial }{{\partial x}}\left( {D_{12}^{(k)}\frac{{\partial {C_{2,k}}}}{{\partial x}}} \right),\] | (1) |
| \[\frac{{\partial {C_{2,k}}}}{{\partial t}} = \frac{\partial }{{\partial x}}\left( {D_{21}^{(k)}\frac{{\partial {C_{1,k}}}}{{\partial x}}} \right) + \frac{\partial }{{\partial x}}\left( {D_{22}^{(k)}\frac{{\partial {C_{2,k}}}}{{\partial x}}} \right),\] | (2) |
где индекс k = p, ph, m и соответствует областям Fe + C, FexAly и Al(C, Fe); С1,k – концентрация железа; С2,k – концентрация углерода в разных областях; \(D_{ij}^{(k)}\) – парциальные диффузионные коэффициенты.
В центре частицы выполняется условие симметрии:
| \[x = 0:\frac{{\partial {C_{1,p}}}}{{\partial x}} = 0;\,\,\,\frac{{\partial {C_{2,p}}}}{{\partial x}} = 0.\] | (3) |
Условия на границах раздела фаз следующие:
\[x = {x_1}(t):{C_{1,p}} = {C_{10}},\,\,\,{C_{2,p}} = {C_{20}},\] \[{C_{1,ph}} = {\varphi _1},{\rm{ }}{C_{2,ph}} = {\gamma _1}{C_{2,p}} \equiv {\gamma _1}{C_{20}},\] \[\left( {{C_{1,p}} - {C_{1,ph}}} \right)\frac{{d{x_1}}}{{dt}} = - {J_{1,ph}}\] или \[\left( {{C_{10}} - {\varphi _1}} \right)\frac{{d{x_1}}}{{dt}} = - {J_{1,ph}},\] | (4) |
где С10 , С20 – начальные концентрации в частицах железа и углерода соответственно; φ1 – предел растворимости железа в переходной зоне, соответствующий соединению Fe3Al;
\[x = {x_2}(t):{C_{1,ph}} = {\varphi _2},\,\,\,{C_{1,m}} = 0,\] \[\left( {{C_{1,ph}} - {C_{1,m}}} \right)\frac{{d{x_2}}}{{dt}} = {J_{1,ph}}\] или \[{\varphi _2}\frac{{d{x_2}}}{{dt}} = {J_{1,ph}},\] | (5) |
| \[ - {D_{21}}\frac{{\partial {C_{1,ph}}}}{{\partial x}} - {D_{22}}\frac{{\partial {C_{2,ph}}}}{{\partial x}} = - {D_m}\frac{{\partial {C_{2,m}}}}{{\partial x}},\] | (6) |
| \[{C_{2,ph}}{\gamma _2} = {C_{2,m}},\] | (7) |
где φ2 – предел растворимости железа в переходной зоне, который соответствует соединению FeAl3 и зависит от концентрации углерода следующим образом:
| \[{\varphi _2} = {\varphi _{20}}\left( {1 - \beta {C_{2,ph}}} \right).\] |
На внешней границе установлено условие непроницаемости:
| \[x = {R_m}:\frac{{\partial {C_{2,m}}}}{{\partial x}} = 0.\] | (8) |
Выражения для диффузионных потоков в области растущей новой фазы имеют вид
| \[{J_{1,ph}} = - {D_{11}}\frac{{\partial {C_{1,ph}}}}{{\partial x}} - {D_{12}}\frac{{\partial {C_{2,ph}}}}{{\partial x}},\] | (9) |
| \[{J_{2,ph}} = - {D_{21}}\frac{{\partial {C_{1,ph}}}}{{\partial x}} - {D_{22}}\frac{{\partial {C_{2,ph}}}}{{\partial x}}.\] | (10) |
В начальный момент времени имеем
t = 0: C1, p = C1, p0 = 0,995, C2, p = C2, p0 = 0,005,
C1, m = 0, C2, m = 0, C1, ph = 0, C2, ph = 0,
x1 = x10 = R0 , x2 = x20 = R0 .
Учитывая малую растворимость алюминия в железе, а железа в алюминии, допустим, что в области Fe + C (слева от подвижной границы X1(t)) концентрации железа и углерода неизменны, а в область Al (справа от X2(t)) может диффундировать только углерод. Тогда слева от подвижной границы X1(t) имеем
| C1, p = C1, p0 , C2, p = C2, p0 , | (11) |
а справа от X2(t)
| \[\frac{{\partial {C_{2,m}}}}{{\partial t}} = {D_m}\frac{{{\partial ^2}{C_{2,m}}}}{{\partial {x^2}}}.\] | (12) |
Далее верхний индекс «k» при коэффициентах диффузии в растущей фазе опускаем.
Для построения аналитического решения и качественного анализа воспользуемся квазистатическим приближением и примем в уравнениях (1), (2) и (12)
| \[\frac{{\partial {C_{1,ph}}}}{{\partial t}} = 0,{\rm{ }}\frac{{\partial {C_{2,ph}}}}{{\partial t}} = 0,{\rm{ }}\frac{{\partial {C_{2,m}}}}{{\partial t}} = 0.\] |
Тогда формулы (1) и (2) примут вид
\[\frac{d}{{dx}}\left( {{D_{11}}\frac{{d{C_{1,ph}}}}{{dx}}} \right) + \frac{d}{{dx}}\left( {{D_{12}}\frac{{d{C_{2,ph}}}}{{dx}}} \right) = 0,\] \[\frac{d}{{dx}}\left( {{D_{21}}\frac{{d{C_{1,ph}}}}{{dx}}} \right) + \frac{d}{{dx}}\left( {{D_{22}}\frac{{d{C_{2,ph}}}}{{dx}}} \right) = 0.\] |
Эти уравнения эквивалентны следующим:
| \[\frac{d}{{dx}}\left( {\frac{{d{C_{1,ph}}}}{{dx}}} \right) = 0,{\rm{ }}\frac{d}{{dx}}\left( {\frac{{d{C_{2,ph}}}}{{dx}}} \right) = 0.\] |
Их решение имеет вид
| C1, ph (x) = A1x + B1 и C2, ph (x) = A2x + B2 , | (13) |
где A1 , A2 , B1 , B2 – постоянные интегрирования.
Подставив решение (13) в граничные условия для концентраций, получим следующую систему линейных алгебраических уравнений:
| \[x = {x_1}(t):{\varphi _1} = {A_1}{x_1} + {B_1},{\rm{ }}{\gamma _1}{C_{20}} = {A_2}{x_1} + {B_2},\] | (14) |
| \[x = {x_2}(t):\left( {{\varphi _{20}} - {\varphi _{20}}{\beta _2}\left[ {{A_2}{x_2} + {B_2}} \right]} \right) = {A_1}{x_2} + {B_1},\] | (15) |
| D21 A1 + D22 A2 = 0. | (16) |
Решение будет следующим:
\[{A_1} = {D_{22}}\alpha \frac{1}{{{x_2} - {x_1}}},{\rm{ }}{B_1} = {\varphi _1} - {D_{22}}\alpha \frac{{{x_1}}}{{{x_2} - {x_1}}},\] \[{A_2} = - {D_{21}}\alpha \frac{1}{{{x_2} - {x_1}}},{\rm{ }}{B_2} = {\gamma _1}{C_{20}} + {D_{21}}\alpha \frac{{{x_1}}}{{{x_2} - {x_1}}},\] |
где
| \[\alpha = \frac{{{\varphi _1} - {\varphi _{20}}\left( {1 - \beta {\gamma _1}{C_{20}}} \right)}}{{{\varphi _{20}}\beta {D_{21}} + {D_{22}}}}.\] | (17) |
Тогда выражение для потока (9) принимает вид
| \[{J_{1,ph}} = - {D_{11}}{A_1} - {D_{12}}{A_2} = - \frac{{\alpha \Delta }}{{{x_2} - {x_1}}},\] | (18) |
где Δ = D11D22 − D12D21 .
Далее находим уравнения для подвижных границ из условий диффузионных потоков (4) и (5):
\[\left( {{C_{10}} - {\varphi _1}} \right)\frac{{d{x_1}}}{{dt}} = \frac{{\alpha \Delta }}{{{x_2} - {x_1}}},\] \[{\varphi _{20}}\left( {1 - \beta {C_{2,ph}}} \right)\frac{{d{x_2}}}{{dt}} = - \frac{{\alpha \Delta }}{{{x_2} - {x_1}}}.\] | (19) |
Подставляя в (13) выражения для постоянных интегрирования, получим выражение для C2, ph :
| \[{C_{2,ph}}({x_2}) = - {D_{21}}\alpha \frac{1}{{{x_2} - {x_1}}}{x_2} + {\gamma _1}{C_{20}} + {D_{21}}\alpha \frac{{{x_1}}}{{{x_2} - {x_1}}} = {\gamma _1}{C_{20}} - {D_{21}}\alpha .\] |
В результате находим
| \[{\varphi _{20}}\left( {1 - \beta \left[ {{\gamma _1}{C_{20}} - {D_{21}}\alpha } \right]} \right)\frac{{d{x_2}}}{{dt}} = - \frac{{\alpha \Delta }}{{{x_2} - {x_1}}}.\] | (20) |
Из формул (19) и (20) следует
| \[\chi \frac{{d{x_1}}}{{d{x_2}}} = - 1,\] |
где \(\chi = \frac{{{C_{10}} - {\varphi _1}}}{{{\varphi _{20}}\left( {1 - \beta \left[ {{\gamma _1}{C_{20}} - {D_{21}}\alpha } \right]} \right)}}\), отсюда следует
| x2 = –χx1 + F′. | (21) |
В начальный момент времени обе границы находятся в точке R0 :
R0 = –χ R0 + F′,
тогда
F′ = R0 (1 + χ), x2 = –χx1 + R0 (1 + χ),
\[\left( {{C_{10}} - {\varphi _1}} \right)\frac{{d{x_1}}}{{dt}} = \frac{{\alpha \Delta }}{{\left( {{R_{\rm{0}}} - {x_1}} \right)\left( {\chi + 1} \right)}}.\]
Тогда выражение для границы x1 примет вид
| \[\frac{{{{\left( {{x_1} - {R_0}} \right)}^2}}}{2} = - \frac{{\alpha \Delta t}}{{\left( {{C_{10}} - {\varphi _1}} \right)\left( {1 + \chi } \right)}} + F'',\] | (22) |
где F″ – константа интегрирования. Из начальных условий имеем F″ = 0.
Таким образом, границы движутся по параболическому закону, однако на их скорость влияют перекрестные диффузионные потоки и она изменяется вследствие изменения области гомогенности интерметаллидной фазы. Это иллюстрирует рис. 4, где представлены зависимости положения границ от времени (верхние кривые соответствуют границе x2 , нижние – x1 ).
Рис. 4. Положение границ в условиях плоской частицы |
В расчетах принято: D11 = 3,63·10\(^-\)10, D12 = 2,47·10\(^-\)12, D22 = 3,32·10\(^-\)11,
D21 = 1,84·10\(^-\)12 м2/с, R0 = 100 мкм.
Заметим, что если имеются только перекрестные потоки, то из выражения (22) следует
| \[\frac{{{{\left( {{x_1} - {R_0}} \right)}^2}}}{2} = - \frac{{{\varphi _1} - {\varphi _{20}}}}{{{D_{22}}}}{\varphi _{20}}\frac{{{D_{11}}{D_{22}} - {D_{12}}{D_{21}}}}{{\left( {{C_{10}} - {\varphi _1}} \right)\left( {{C_{10}} - {\varphi _1} + {\varphi _{20}}} \right)}}t,\] |
а если примесь отсутствует, то
| \[\frac{{{{\left( {{x_1} - {R_0}} \right)}^2}}}{2} = - \frac{{{D_{11}}\left( {{\varphi _1} - {\varphi _{20}}} \right){\varphi _{20}}t}}{{\left( {{C_{10}} - {\varphi _1}} \right)\left( {{C_{10}} - {\varphi _1} + {\varphi _{20}}} \right)}}.\] |
Таким образом, наличие перекрестных диффузионных потоков в зависимости от знака произведения D12 D21 может приводить как к ускорению, так и замедлению движения границ, т.е. к ускорению или замедлению фазообразования. А расширение области гомогенности фазы всегда действует в одну сторону. Это говорит о том, что в условиях эксперимента скорее реализуется первый вариант с D12 D21 > 0.
При учете изменения величины φ1 с концентрацией углерода решение получается аналогично.
2. Во втором варианте примем, что частица имеет сферическую форму.
В сферической системе координат уравнения диффузии для переходного слоя имеют вид
\[\frac{{\partial {C_{1,ph}}}}{{\partial t}} = \frac{1}{{{r^2}}}\frac{\partial }{{\partial r}}\left( {{r^2}{D_{11}}\frac{{\partial {C_{1,ph}}}}{{\partial r}}} \right) + \frac{1}{{{r^2}}}\frac{\partial }{{\partial r}}\left( {{r^2}{D_{12}}\frac{{\partial {C_{2,ph}}}}{{\partial r}}} \right),\] \[\frac{{\partial {C_{2,ph}}}}{{\partial t}} = \frac{1}{{{r^2}}}\frac{\partial }{{\partial r}}\left( {{r^2}{D_{21}}\frac{{\partial {C_{1,ph}}}}{{\partial r}}} \right) + \frac{1}{{{r^2}}}\frac{\partial }{{\partial r}}\left( {{r^2}{D_{22}}\frac{{\partial {C_{2,ph}}}}{{\partial r}}} \right),\] |
где r – радиальная координата.
В квазистационарном приближении имеем
\[\frac{1}{{{r^2}}}\frac{d}{{dr}}\left( {{r^2}{D_{11}}\frac{{d{C_{1,ph}}}}{{dr}}} \right) + \frac{1}{{{r^2}}}\frac{d}{{dr}}\left( {{r^2}{D_{12}}\frac{{d{C_{2,ph}}}}{{dr}}} \right) = 0,\] \[\frac{1}{{{r^2}}}\frac{d}{{dr}}\left( {{r^2}{D_{21}}\frac{{d{C_{1,ph}}}}{{dr}}} \right) + \frac{1}{{{r^2}}}\frac{d}{{dr}}\left( {{r^2}{D_{22}}\frac{{d{C_{2,ph}}}}{{dr}}} \right) = 0.\] |
Граничные условия, как и решение, аналогичны предыдущей задаче. Распределение концентраций имеет вид
| \[{C_{1,ph}}(r) = - \frac{{{A_1}}}{r} + {B_1},{\rm{ }}{C_{2,ph}}(r) = - \frac{{{A_2}}}{r} + {B_2},\] | (23) |
где
\[{A_1} = - \alpha {D_{22}}\frac{{{x_1}{x_2}}}{{{x_1} - {x_2}}},{\rm{ }}{B_1} = - \alpha {D_{22}}\frac{{{x_2}}}{{{x_1} - {x_2}}} + {\varphi _1},\] \[{A_2} = \alpha {D_{21}}\frac{{{x_1}{x_2}}}{{{x_1} - {x_2}}},{\rm{ }}{B_2} = \alpha {D_{21}}\frac{{{x_2}}}{{{x_1} - {x_2}}} + {\gamma _1}{C_{20}}.\] | (24) |
Выражение для потока, аналогичное (9), с учетом найденного решения (23), (24) принимает вид
\[{J_{1,ph}} = - \left( {{D_{11}}\frac{{{A_1}}}{{{r^2}}} + {D_{12}}\frac{{{A_2}}}{{{r^2}}}} \right) = \] \[ = - \frac{1}{{{r^2}}}\alpha \frac{{{x_1}{x_2}}}{{{x_1} - {x_2}}}\left( { - {D_{11}}{D_{22}} + {D_{12}}{D_{21}}} \right) = \Delta \alpha \frac{{{x_1}{x_2}}}{{{x_1} - {x_2}}}\frac{1}{{{r^2}}}.\] | (25) |
Следовательно, из условий, аналогичных (4) и (5), находим уравнение для подвижных границ и соотношение между ними:
| \(\chi \frac{{d{x_1}}}{{d{x_2}}} = - \frac{{x_2^2}}{{x_1^2}}\) и \[{x_2} = - \sqrt[3]{\chi }{x_1} + F',\] |
где
\[F' = {R_0}\left( {1 + \sqrt[3]{\chi }} \right),\] \[\chi = \frac{{{C_{10}} - {\varphi _1}}}{{{\varphi _{20}}\left( {1 - \beta \left[ {{\gamma _1}{C_{20}} - {D_{21}}\alpha } \right]} \right)}}.\] |
Таким образом, опять получаем параболический закон, отличающийся от предыдущего только степенью влияния параметров:
| \[\frac{{{{\left( {{R_0} - {x_1}} \right)}^2}}}{2} = - \frac{{\alpha \Delta t}}{{\left( {{C_{10}} - {\varphi _1}} \right)\left( {1 + \sqrt[3]{\chi }} \right)}}.\] |
Рис. 5 иллюстрирует различие скоростей движения границ раздела фаз для частиц разной формы.
Рис. 5. Изменение положения границ со временем |
Заключение
Таким образом, показано, что при взаимодействии частиц измельченной стальной стружки с порошковым алюминием в условиях вакуумного спекания, несмотря на экзотермическую реакцию синтеза интерметаллидов, фазовые превращения не происходят в полном объеме. Наряду с синтезированными фазами присутствуют фазы исходных компонентов.
С помощью модельных задач показано, что наличие примеси в стружке может быть причиной изменения скорости роста фаз как за счет появления перекрестных диффузионных потоков, так и вследствие изменения размеров области гомогенности растущей фазы. Эффект проявляется для частиц как плоской, так и сферической форм.
Список литературы
1. Ровин С.Л., Калиниченко А.С., Ровин Л.Е. Возвращение дисперсных металлоотходов в производство. Литье и металлургия. 2019;(1):45–48. https://doi.org/10.21122/1683-6065-2019-1-45-48
2. Chang J.I., Lin J.J., Huang J.S., Chang Y.M. Recycling oil and steel from grinding swarf. Resources, Conservation and Recycling. 2006;49(2):191–201. https://doi.org/10.1016/j.resconrec.2006.03.014
3. Дьяконов О.М. Получение металлургических брикетов на основе стружко-порошковых композиций горячим прессованием. Литье и металлургия. 2011;(4):129–137.
4. Andersson A., Gullberg A., Kullerstedt A., Sandberg E., Andersson M., Ahmed H., Sundqvist-Ökvist L., Björkman B. A holistic and experimentally-based view on recycling of off-gas dust within the integrated steel plant. Metals. 2018;8(10):760. https://doi.org/10.3390/met8100760
5. Ровин С.Л., Ровин Л.Е., Заяц Т.М., Валицкая О.М. Переработка стружки черных металлов. Литье и металлургия. 2017;89(4):94–101. https://doi.org/10.21122/1683-6065-2017-4-94-101
6. Hankel J., Jager S., Weber S. Development of a recycling strategy for grinding sludge using supersolidus liquid phase sintering. Journal of Cleaner Production. 2020;263:121501. https://doi.org/10.1016/j.jclepro.2020.121501
7. Дьяконов О.М. Исследование физико-химических и механических свойств стальной и чугунной стружки. Литье и металлургия. 2009;(4):161–173.
8. Логинов Ю.Н., Загиров Н.Н., Иванов Е.В. Оценка уровня упрочнения стружки из алюминиевого сплава, предназначенной для последующей обработки давлением. Обработка металлов (технология, оборудование, инструменты). 2021;23(1):45–55.
9. Mahmooda K., Ul Haq Syed W., Pinkerton A.J. Innovative reconsolidation of carbon steel machining swarf by laser metal deposition. Optics and Lasers in Engineering. 2011;49(2):240–247. https://doi.org/10.1016/j.optlaseng.2010.09.014
10. Gnatko M., Li C., Arnold A., Freidrich B. Purification of aluminium cast alloy melts through precipitation of Fe-containing intermetallic compounds. Metals. 2018;8(10):796. https://doi.org/10.3390/met8100796
11. Shahid R.N., Scudino S. Strengthening of Al–Fe3Al composites by the generation of harmonic structures. Scientific Reports. 2018;8:6484. https://doi.org/10.1038/s41598-018-24824-y
12. Tomida S., Nakata K. Fe–Al composite layers on aluminum alloy formed by laser surface alloying with iron powder. Surface and Coatings Technology. 2003;174-175:559–563. https://doi.org/10.1016/S0257-8972(03)00698-4
13. Minamino Y., Koizumi Y., Tsuji N., Hirohata N., Mizuuchi K., Ohkanda Y. Microstructures and mechanical properties of bulk nanocrystalline Fe–Al–C alloys made by mechanically alloying with subsequent spark plasma sintering. Science and Technology of Advanced Materials. 2004;5(1-2):133–143. https://doi.org/10.1016/j.stam.2003.11.004
14. Najafi A., Movahedi M., Yarandi A.S. Properties–microstructure relationship in Al–Fe in situ composite produced by friction stir processing. Proceedings of the Institution of Mechanical Engineers, Part L: Journal of Materials: Design and Applications. 2019;233(10):1955–1965. https://doi.org/10.1177/1464420718803752
15. Kopec M., Jóźwiak S., Kowalewski Z. Fe–Al based composite reinforced with ultra-fine Al2O3 oxides for high temperature applications. Journal of Theoretical and Applied mechanics. 2021;59(3):509–513. https://doi.org/10.15632/jtam-pl/138322
16. Kostov A., Friedrich B., Zivković D. Thermodynamic calculations in alloys Ti–Al, Ti–Fe, Al–Fe and Ti–Al–Fe. Journal of Mining and Metallurgy, Section B: Metallurgy. 2008;44(1):49–61. https://doi.org/10.2298/JMMB0801049K
17. Диаграммы состояния двойных металлических систем: справочник. В 3 т. Т. 1 / Под ред. Н.П. Лякишева. М: Машиностроение, 1996. 991 с.
18. Jäger S., Weber S. Upcycling strategy of grinding swarf by super solidus liquid phase sintering. Procedia CIRP. 2020;90:546–551. https://doi.org/10.1016/j.procir.2020.01.079
19. Wierzba B. Phase competition in ternary Ti–Ni–Al system. Physica A: Statistical Mechanics and its Applications. 2016;454:110–116. https://doi.org/10.1016/j.physa.2016.02.068
20. Ji Y., Abernathy H.W., Chen L.-Q. Thermodynamic models of multicomponent nonstoichiometric solution phases using internal process order parameters. Acta Materialia. 2022;223:117462. https://doi.org/10.1016/j.actamat.2021.117462
21. Knyazeva A.G. Difusion following the vacancy mechanism in materials with large number of internal surfaces. Chemistry for Sustainable Development. 2005;13(2): 233–242.
22. Belova I.V., Murch G.E. Analysis of interdiffusion data in multicomponent alloys to extract fundamental diffusion information. Journal of Phase Equilibria and Diffusion. 2006;27(6): 629–637. https://doi.org/10.1007/BF02736565
23. Svoboda J., Fischer F.D., Abart R. Modeling of diffusional phase transformation in multi-component systems with stoichiometric phases. Acta Materialia. 2010;58(8):2905–2911. https://doi.org/10.1016/j.actamat.2010.01.019
Об авторах
Е. Н. КоростелеваРоссия
Елена Николаевна Коростелева – кандидат технических наук, старший научный сотрудник ИФПМ СО РАН.
634055, Томск, Академический пр-т, 2/46
А. Г. Князева
Россия
Анна Георгиевна Князева – доктор физико-математических наук, профессор, главный научный сотрудник ИФПМ СО РАН.
634055, Томск, Академический пр-т, 2/46
М. А. Анисимова
Россия
Мария Александровна Анисимова – кандидат физико-математических наук, младший научный сотрудник ИФПМ СО РАН.
634055, Томск, Академический пр-т, 2/46
И. О. Николаев
Россия
Иван Олегович Николаев – инженер ИФПМ СО РАН.
634055, Томск, Академический пр-т, 2/46
Рецензия
Для цитирования:
Коростелева Е.Н., Князева А.Г., Анисимова М.А., Николаев И.О. Роль примесей в изменении фазового состава в системе Al–Fe–C при спекании. Известия вузов. Порошковая металлургия и функциональные покрытия. 2023;17(2):5-13. https://doi.org/10.17073/1997-308X-2023-2-5-13
For citation:
Korosteleva E.N., Knyazeva A.G., Anisimova M.A., Nikolaev I.O. The impact of impurities on the Al–Fe–C system phase composition changes during sintering. Powder Metallurgy аnd Functional Coatings (Izvestiya Vuzov. Poroshkovaya Metallurgiya i Funktsional'nye Pokrytiya). 2023;17(2):5-13. https://doi.org/10.17073/1997-308X-2023-2-5-13
JATS XML