Влияние передаточного отношения на энергосиловые условия столкновения размольных тел в планетарной мельнице

Введение

Механическая обработка (МО) твердых веществ используется для инициации изменения скорости химических и физико-химических процессов, необходимых для механохимического синтеза, механического легирования, механической активации и т.д [1]. Обычно МО проводят в аттриторах, планетарных, вибрационных и шаровых мельницах. Принцип действия этих устройств основан на многократном импульсном механическом воздействии размольных тел на вещество, которое обеспечивает передачу в него механической энергии [2]. При всем разнообразии видов механического воздействия на вещество в основе лежат удар, сдвиг и их комбинации в разных соотношениях, которые зависят от типа устройства и режима его работы [3]. При этом вид механического воздействия, способствующего механохимическим превращениям, оказывает явное влияние на их характер [4].

Обработка в планетарных мельницах нашла широкое применение для решения различных технологических задач, состоящих, например, в механическом легировании/активации, синтезе композиционных порошковых смесей, переработке стружечных отходов и т.д. [5–7]. Принимая во внимание различие данных технологических задач, их эффективная реализация хотя и возможна c помощью одного и того же оборудования, в данном случае планетарной мельницы, но очевидно требует использования различных технологических параметров МО. К ним следует отнести форму и размер размольных тел, коэффициент заполнения ими рабочей камеры, отношение массы обрабатываемого вещества к массе размольных тел, передаточное отношение и частоту вращения солнечного колеса. Подбор этих параметров в большинстве случаев осуществляется эмпирически, методом проб и ошибок, что является весьма трудоемким, а иногда и нереализуемым процессом. Для научно обоснованного их назначения необходимо установление связи между данными параметрами, количеством передаваемой механической энергии и характеристиками обработанного вещества. К последним, в зависимости от задачи, можно отнести гранулометрический и фазовый составы, размер структурных составляющих и т.п. Численное определение передаваемой механической энергии, с учетом перечисленных факторов, влияющих на механику процесса, возможно на основе математического моделирования движения размольных тел, например, с использованием метода дискретных элементов [8–11].

Другим немаловажным направлением исследований является экспериментальное изучение кинематики движения размольных тел в планетарной мельнице в зависимости от параметров МО, которое проводят, например, с помощью высокоскоростной видеосъемки [10; 12]. При этом комплексные расчетно-экспериментальные исследования позволяют дополнить данные о кинематике движения энергосиловыми характеристиками столкновений размольных тел между собой и со стенками рабочей камеры. Это обеспечивает более полное понимание процессов, протекающих при МО, позволяет прогнозировать характеристики получаемого вещества в зависимости от условий обработки и будет способствовать разработке рациональной технологии, обеспечивающей повторяемость получаемых свойств с учетом использования различного оборудования и его масштабируемости.

Цель данной работы состоит в разработке, численной реализации и валидации модели движения размольных тел в планетарной мельнице, а также в исследовании влияния передаточного отношения на характер движения и энергосиловые характеристики столкновения размольных тел.

Описание методик экспериментального
и теоретического исследований

При проведении экспериментальной части исследования использовали лабораторную планетарную мельницу «Activator-2S» (машиностроительный завод «Активатор», г. Новосибирск) и высокоскоростную видеокамеру «Phantom Miro M310» (Vision Research Inc., США). Планетарная мельница имеет две цилиндрические рабочие камеры, расположенные вертикально на солнечном колесе. В одну из рабочих камер помещали 12 стальных размольных тел в форме шара диаметром 9 мм. Для ограничения возможности вертикального перемещения размольных тел в рабочей камере высота последней составляла 1,2 диаметра шара. Особенностью конструкции данной мельницы является наличие двух независимых электродвигателей, которые приводят в движение со скоростями W и w солнечное колесо и рабочую камеру соответственно. Управление скоростями разнонаправленного вращения осуществляется с помощью частотных преобразователей. Видеокамера была размещена над мельницей коаксиально вертикальной оси солнечного колеса (см. рис. 1).

Для видеосъемки стальные крышки рабочих камер были заменены на прозрачные. Скорость записи во всех экспериментах была 2000 кадров в секунду. Высокоскоростную съемку проводили для 4-х значений отношения скоростей вращения рабочей камеры и солнечного колеса (K = w/W), равных 1,0; 1,2; 1,5; 2,0. При этом варьировали только скорость вращения рабочей камеры, а скорость вращения солнечного колеса во всех опытах была постоянной и составляла 694 об/мин.

В дополнение к экспериментальным исследованиям движения размольных тел выполняли моделирование процесса с использованием метода дискретных элементов. В данном методе динамика поступательного и вращательного движений размольных тел в рабочей камере планетарной мельницы описывается с помощью пошагового алгоритма с постоянным обновлением положения тел и стенок. При этом для каждого i-го размольного тела решается система из двух уравнений поступательного и вращательного движения, имеющих следующий вид:

Первое уравнение описывает поступательное движение центра масс размольных тел. Величины m_i и v_i – масса и скорость i-го тела, t – время, g – ускорение свободного падения. Первое слагаемое в правой части равенства учитывает действие на данное размольное тело сил гравитации, второе – взаимодействие между телами, а последнее – взаимодействие размольного тела со стенками рабочей камеры. Начальные скорости поступательного и вращательного движений считаются заданными. Поскольку масса рабочей камеры существенно превышает совокупную массу размольных тел, можно пренебречь влиянием взаимодействия стенок с телами на движение камеры и считать, что закон движения стенок известен.

Учет вращательного движения размольных тел в планетарной мельнице обеспечивается вторым уравнением системы (1). Скалярная переменная I_i используется для обозначения момента инерции, а векторные переменные ω_i, T_ij и ${\mathbf{T}}_i^b$ обозначают угловую скорость и моменты сил, возникающие при взаимодействии данного размольного тела с другим телом с индексом j либо со стенкой рабочей камеры. Слагаемое M_i введено для учета сил трения качения, действующих на размольные тела.

Для учета взаимодействия между i-м и j-м телами введены силы F_ij и моменты сил T_ij, входящие в уравнение (1) под знаком суммы. Суммирование по всем возможным значениям j ≠ i позволяет исключить самодействие. При этом учитывается только взаимодействие контактирующих размольных тел. Для тел, расположенных друг от друга на большем расстоянии, сила взаимодействия полагается равной нулю.

При расчете сил взаимодействия между размольными телами и их моментов в настоящей работе применялась теория Г. Герца, дополненная теорией сдвига Р. Миндлина (модель Герца–Миндлина) [13]. Характер взаимодействия не может считаться абсолютно упругим, поэтому для учета потерь энергии при столкновении размольных тел вводится, кроме силы контакта, дополнительная диссипативная сила. Расчет столкновения размольных тел со стенкой рабочей камеры выполняется по аналогичной модели, однако, поскольку радиус рабочей камеры существенно превышает радиус каждого из тел, кривизна поверхности стенки не учитывается.

Параметрами модели являются физико-механические характеристики материала размольных тел и рабочей камеры, а также коэффициенты, характеризующие их контактное взаимодействие. К последним относятся коэффициенты реституции (e_R), статического трения (µ_S) и трения качения (µ_R). Если физико-механические характеристики для большинства конструкционных материалов являются справочными данными, то определение коэффициентов, характеризующих их контактное взаимодействие, представляет собой самостоятельную экспериментальную задачу, которую, например, решали в работах [14–16]. Следует учесть, что данные коэффициенты могут зависеть, в том числе, от размера и правильности формы (отклонения от формы шара) размольных тел, шероховатости поверхности размольных тел и рабочей камеры и т.д., а поэтому требуют уточнения, которое в настоящей работе проводили методом подгонки модели под данные эксперимента.

В качестве начального приближения, учитывая рекомендации работ [17; 18], принимали e_R = 0,85, µ_S = 0,45 и µ_R = 0,02. Для подгонки была проведена серия численных расчетов, имитирующих условия эксперимента, в которых изменяли значения коэффициентов, характеризующих контактное взаимодействие. В качестве критерия близости экспериментальных и расчетных результатов было принято соответствие картин положения (структуры мгновенных изображений) размольных тел в рабочей камере. Валидацию модели выполняли путем соотнесения площадей экспериментальной и расчетной структур системы размольных тел для 8 положений рабочей камеры на установившемся режиме работы планетарной мельницы. Результаты подгонки считали удовлетворительными, если расхождение экспериментальных и расчетных данных (Δ) не превышало 15 % для одних и тех же значений коэффициентов, характеризующих контактное взаимодействие.

Результаты и их обсуждение

В табл. 1 представлены типичные мгновенные изображения размольных тел, полученные экспериментально (столбец «Эксперимент») и путем моделирования (столбец «Модель») для различных вариантов отношения скоростей вращения рабочей камеры и солнечного колеса. Кроме того, в табл. 1 показаны изображения площадей экспериментальной и расчетной структур многочастичной системы (столбец «Сравнение»). И, наконец, в табл. 1 приведены усредненные для 8 положений рабочей камеры числовые данные о несоответствии этих площадей (Δ), являющиеся погрешностью разработанной модели и характеризующие ее адекватность.

Таблица 1. Сопоставление результатов эксперимента и расчетных данных K = w/W Эксперимент Модель Сравнение Δ, % 1,0 12,4 1,2 11,9 1,5 9,1 2,0 12,2

Анализ представленных в табл. 1 результатов эксперимента и расчетных данных позволяет сделать вывод об их разумном соответствии. Расхождение не превышает 13 %. При этом подгоночные параметры были едины для различных вариантов отношения скоростей вращения рабочей камеры и солнечного колеса. Значения коэффициентов (подгоночных параметров), характеризующих контактное взаимодействие, составили e_R = 0,75, µS = 0,21 и µ_R = 0,023. Необходимо отметить, что если значения e_R и µ_R достаточно близки или совпадали с используемыми при моделировании в работах [19; 20], то значение µ_S значительно отличалось (более чем в 3 раза). Вместе с тем параметр µ_S оказывает существенное влияние не только на характер движения размольных тел [10], но и на количественные значения энергосиловых характеристик столкновений, что в значительной мере определяет их достоверность. Таким образом, разработанная модель является адекватной и может быть использована для изучения влияния передаточного отношения на характер движения размольных тел в ходе высокоэнергетического шарового размола и энергосиловые параметры процесса обработки.

Далее с помощью разработанной модели было изучено влияние передаточного отношения на характер движения размольных тел в рабочей камере. Анализ результатов моделирования показывает, что изменение величины K от 1,0 до 1,5 практически не влияет на кинематику движения размольных тел. Напротив, при увеличении K до 2,0 характер движения размольных тел изменяется значительно. В первом случае, при K = 1,0÷1,5, реализуется режим движения размольных тел, при котором происходит циклическое перекатывание тел с первого на второй ряд. При этом обработка материала может происходить как истиранием между стенкой рабочей камеры и размольными телами, так и соударениями размольных тел при перекатывании. Во втором случае, при K = 2,0, появляются размольные тела, которые свободно меняют свое положение относительно центра рабочей камеры. Поэтому можно наблюдать трехрядное перекатывание, которое реализуется путем одновременного забрасывания на второй ряд двух и более размольных тел, что ведет к формированию третьего ряда (см. табл. 1). Т.е. кроме режима перекатывания частично реализуется и режим свободного полета размольных тел, при котором некоторые размольные тела отделяются от стенки и выбрасываются в свободное пространство рабочей камеры, осуществляя свободный полет до момента столкновения с другим размольным телом или стенкой рабочей камеры. Для такого режима движения характерны соударения наибольшей интенсивности. Однако количество соударений по сравнению с режимом перекатывания, по всей видимости, должно снижаться.

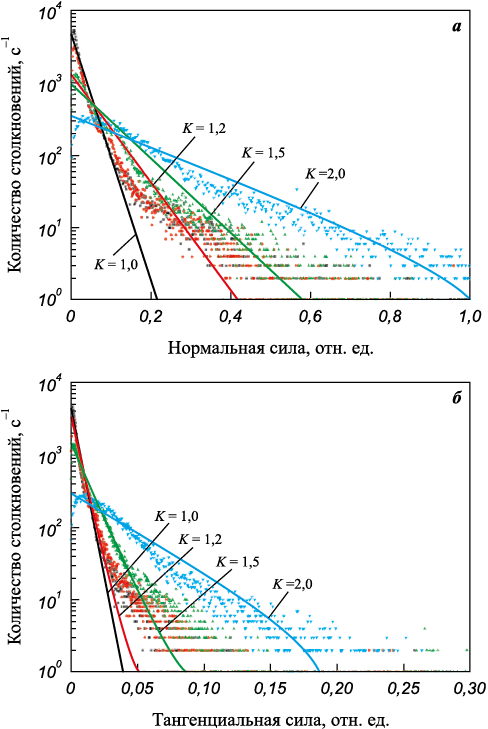
Также были получены оценки влияния передаточного отношения на изменение силовых характеристик контактного взаимодействия размольных тел друг с другом и со стенками рабочей камеры. На рис. 2 представлены нормированные расчетные данные о распределении количества столкновений по силе сжатия и усилию сдвига для различных передаточных отношений.

Можно видеть, что увеличение передаточного отношения способствует росту нормальной силы при столкновениях (см. рис. 2, а). Причем изменение K от 1 до 2 ведет к повышению максимальной нормальной силы при столкновениях в ~5 раз. При этом наблюдается значительная дифференциация столкновений по усилиям. Так, если принять условное деление общего числа столкновений, в зависимости от усилия, на низкоинтенсивные (F < 0,01), среднеинтенсивные (0,01 < F < 0,1) и высокоинтенсивные (F > 0,1) и провести их сопоставление для различных передаточных отношений (см. табл. 2), то можно заметить, что в случаях K = 1,0÷1,5 основная доля столкновений является среднеинтенсивной. Причем увеличение доли таких столкновений для данного интервала изменения K не превышает 6 %.

В то же время происходит перераспределение столкновений по интенсивности. Так, например, при K = 1,0 установлено, что 32,5 % столкновений являются низкоинтенсивными и только 5,6 % – высокоинтенсивными. При K = 1,5 доля низкоинтенсивных столкновений уже составляет 12,1 %, а высокоинтенсивных – 20,1 %. Однако с увеличением K до 2,0, т.е. с изменением типа движения размольных тел, доля среднеинтенсивных столкновений уменьшается до 42,3 %. Напротив, доля высокоинтенсивных столкновений возрастает и составляет уже 55,3 %, а количество таких столкновений заметно снижается. Качественно схожую картину наблюдали и для усилия сдвига (см. рис. 2, б). Важным является то, что для K = 1,0÷1,5 основная масса столкновений является среднеинтенсивной. И если предположить, что этих усилий достаточно для создания необходимого поля механических напряжений, то активационная обработка частиц вещества может быть одинаково эффективной и при K = 1,0 и при K = 1,5, а обработка при K = 2,0, несмотря на превалирование столкновений с высокой интенсивностью и учитывая снижение их количества, может быть менее эффективной, чем при K = 1,0÷1,5. По всей видимости, режим K = 2,0 более целесообразно использовать при обработке крупноразмерных частиц вещества, требующей бóльших усилий для его деформирования и фрагментирования.

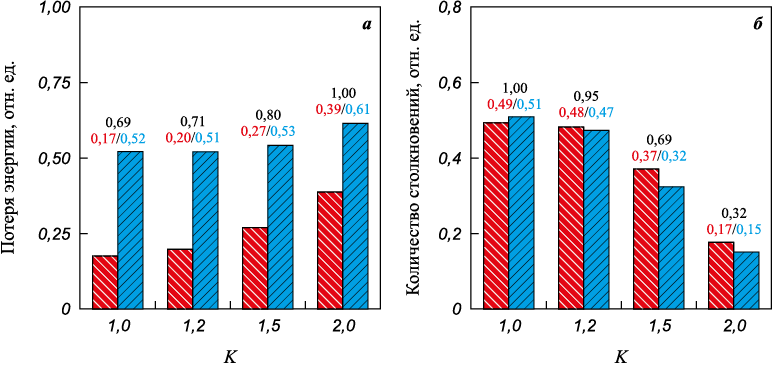
На рис. 3 представлены нормированные данные, характеризующие суммарную потерю энергии при столкновениях «тело–тело» и «тело–камера» для разных передаточных отношений и изменение количества столкновений.

Анализ представленных графических зависимостей показывает, что с ростом передаточного отношения K от 1,0 до 2,0 суммарная потеря энергии при столкновениях «тело–тело» увеличивается на ~30 % (см. рис. 3, а). Однако потеря энергии при столкновениях «тело–камера» для передаточных отношений K от 1,0 до 1,5 практически не изменяется, а для случая K = 2,0 увеличивается лишь на ~13 %. То есть рост суммарной потери энергии при столкновениях в основном происходит за счет изменения (увеличения) потери энергии при столкновениях пар «тело–тело».

Количество столкновений с ростом передаточного соотношения ожидаемо уменьшается (см. рис. 3, б). Причем если при K = 1,0 и 1,2 оно снижается незначительно, то при достижении K = 1,5 и, далее, K = 2,0 – в ~1,5 и ~3,1 раза соответственно. Такое сокращение количества столкновений может приводить к уменьшению вероятности возникновения контактов размольных тел с обрабатываемым веществом, тем самым снижая эффективность обработки. Таким образом, увеличение передаточного отношения ведет к значительному снижению количества столкновений размольных тел с одновременным ростом удельной потери энергии столкновения, который, несмотря на падение количества столкновений, обеспечивает повышение суммарной потери энергии столкновений. Интересным является то, что при обработке смесей микрометрических частиц, с высоким отношением массы размольных тел к массе обрабатываемого вещества, частицы вещества имеют тенденцию собираться у стенки из-за их способности проходить через пустоты между размольными телами [19]. Поэтому, несмотря на увеличение суммарной потери энергии при столкновениях, к которому ведет рост передаточного отношения, использование режимов обработки с K = 2,0 может являться менее эффективным, чем при низких K, так как столкновения «тело–тело» не вносят вклад в обработку, а количество столкновений «тело–камера», несмотря на рост их интенсивности, существенно снижается. По всей видимости, повышение эффективности обработки порошковых смесей за счет использования бóльших значений K может быть достигнуто в случае обработки с низким отношением массы размольных тел к массе вещества, когда частицы вещества располагаются не только у стенок рабочей камеры, но и вокруг ее центра, что обеспечит более эффективное использование столкновений «тело–тело». Другим вариантом рационального использования режима обработки при K = 2,0 является обработка крупноразмерных частиц вещества миллиметрового размера, когда необходимы высокие усилия для деформирования частиц, например при обработке гранульных или стружечных материалов.

Заключение

Разработана, численно реализована и валидирована модель движения размольных тел в планетарной мельнице «Activator-2S». Путем сопоставления расчетных и экспериментальных данных определены параметры модели, обеспечивающие ее адекватность. Анализ модели позволил установить, что с ростом передаточного отношения K в диапазоне от 1,0 до 2,0 снижается доля малоподвижных размольных тел и происходит изменение характера их движения с режима перекатывания на режим перекатывания и свободного полета. Это ведет к увеличению силовых характеристик столкновений размольных тел с одновременным уменьшением их количества. При этом, несмотря на значительную дифференциацию столкновений по усилиям, доля среднеинтенсивных столкновений при K от 1,0 до 1,5 практически не изменяется, а при дальнейшем увеличении K до 2,0 – снижается, повышая долю высокоинтенсивных столкновений. Суммарные потери энергии при столкновениях при изменении K от 1,0 до 2,0 увеличиваются на ~30 %. Однако потери энергии столкновений пары «тело-камера» для K от 1,0 до 1,5 не изменяются, а рост суммарных потерь энергии при столкновениях происходит за счет повышения доли потери энергии при столкновениях пар «тело–тело». Учитывая данные о влиянии передаточного отношения на изменение характера столкновений и энергосиловые характеристики механической обработки, можно рекомендовать режим при K от 1,0 до 1,5 для механической обработки микронных частиц вещества с большим отношением массы размольных тел к массе вещества. Режим с K = 2,0, по всей видимости, будет более рационален в случае механической обработки крупных частиц вещества при решении задачи фрагментирования компонентов смеси. Модель может найти применение для оценки энергосиловых характеристик процесса обработки в планетарных мельницах на этапе разработки технологии.