Influence of gear ratio on the energy-force conditions of grinding body collisions in a planetary mill

Introduction

Mechanical processing (MP) of solid materials is widely used to initiate changes in the rates of chemical and physicochemical processes required for mechanochemical synthesis, mechanical alloying, mechanical activation, and other applications [1]. Typically, MP is performed in attritors, planetary mills, vibratory mills, and ball mills. The operating principle of these devices is based on repeated impulsive mechanical impacts of grinding bodies on the material, enabling the transfer of mechanical energy into it [2]. Despite the variety of mechanical impact types, the primary modes include impact, shear, and their combinations in various proportions, depending on the type of equipment and its operating conditions [3]. Notably, the type of mechanical impact promoting mechanochemical transformations significantly influences their nature [4].

Processing in planetary mills has found widespread application in solving various technological challenges, such as mechanical alloying/activation, synthesis of composite powder mixtures, and recycling of chip waste, among others [5–7]. Considering the diversity of these technological tasks, their efficient execution, while possible with the same equipment (in this case, a planetary mill), evidently requires the use of different MP parameters. These parameters include the shape and size of the grinding media, the filling ratio of the working chamber, the mass ratio of the processed material to the grinding bodies, the gear ratio, and the rotation frequency of the sun wheel. In most cases, the selection of these parameters is performed empirically through trial and error, which can be a labor-intensive and sometimes infeasible process. Scientifically grounded parameter selection requires establishing relationships between these parameters, the amount of mechanical energy transferred, and the characteristics of the processed material. Depending on the task, these characteristics may include the granulometric and phase composition, the size of structural components, and others. Numerical determination of the transferred mechanical energy, considering the aforementioned factors influencing the process mechanics, can be achieved through mathematical modeling of grinding body motion, for example, using the discrete element method (DEM) [8–11].

Another significant research direction involves experimental studies of the kinematics of grinding body motion in a planetary mill as a function of MP parameters, conducted, for instance, using high-speed videography [10; 12]. Comprehensive computational and experimental studies allow the kinematic data to be supplemented with energy-force characteristics of collisions between grinding bodies and the walls of the working chamber. This provides a more complete understanding of the processes occurring during MP, enabling predictions of material properties based on processing conditions and facilitating the development of rational technologies that ensure reproducibility of material properties across various equipment types and scalability.

The aim of this study is to develop, numerically implement, and validate a model of grinding body motion in a planetary mill, as well as to investigate the effect of the gear ratio on the motion pattern and energy-force characteristics of grinding body collisions.

Experimental and theoretical
research methods

In the experimental part of this study, a laboratory planetary mill “Activator-2S” (Activator Mechanical Engineering Plant, Novosibirsk, Russia) and a high-speed video camera “Phantom Miro M310” (Vision Research Inc., USA) were used. The planetary mill is equipped with two cylindrical working chambers positioned vertically on the sun wheel. One of the chambers was loaded with 12 steel grinding bodies in the form of 9 mm-diameter spheres. To limit vertical displacement of the grinding bodies within the working chamber, the chamber height was set at 1.2 times the sphere diameter. A notable design feature of this mill is the presence of two independent electric motors driving the sun wheel and the working chamber at speeds W and w, respectively. The counter-rotational speeds are controlled via frequency converters. The video camera was positioned above the mill, coaxial to the vertical axis of the sun wheel (see Fig. 1).

For the videography, the steel lids of the working chambers were replaced with transparent ones. The recording speed for all experiments was set to 2000 frames per second. High-speed video recording was conducted for four values of the speed ratio of the working chamber to the sun wheel (K = w/W), specifically K = 1.0; 1.2; 1.5; 2.0. In these experiments, only the rotation speed of the working chamber was varied, while the rotation speed of the sun wheel remained constant at 694 rpm.

In addition to the experimental studies of grinding body motion, the process was modeled using the discrete element method (DEM). This method describes the translational and rotational dynamics of grinding bodies in the working chamber of a planetary mill using a stepwise algorithm with constant updates of the positions of the bodies and the chamber walls. For each i-th grinding body, a system of two equations of translational and rotational motion is solved, expressed as follows:

The first equation describes the translational motion of the center of mass of the grinding body. The variables m_i and v_i denote the mass and velocity of the i-th body, t is time, and g is the acceleration due to gravity. The first term on the right-hand side accounts for gravitational forces acting on the grinding body, the second term represents interactions between bodies, and the last term accounts for interactions between the grinding body and the chamber walls. The initial velocities of translational and rotational motion are predefined. Since the mass of the working chamber significantly exceeds the total mass of the grinding bodies, the influence of body-wall interactions on the chamber’s motion can be neglected, and the motion of the chamber walls is assumed to be known.

The rotational motion of the grinding bodies in the planetary mill is described by the second equation in system (1). The scalar variable I_i denotes the moment of inertia, while the vector variables ω_i, T_ij and \({\bf{T}}_i^b\) represent the angular velocity and torques arising from the interactions of the grinding body with other bodies (indexed j) or with the chamber walls. The term M_i accounts for rolling friction forces acting on the grinding bodies.

The interactions between the i-th and j-th bodies are represented by forces F_ij and torques T_ij, included in equation (1) under the summation sign. Summation over all possible values of j ≠ i eliminates self-interaction, considering only contacting grinding bodies. For bodies separated by greater distances, the interaction force is assumed to be zero.

In this study, the calculation of interaction forces and torques between grinding bodies employed Hertz’s theory, supplemented by Mindlin’s shear theory (the Hertz–Mindlin model) [13]. Since the interactions are not perfectly elastic, an additional dissipative force is introduced alongside the contact force to account for energy losses during collisions. Collisions between grinding bodies and the chamber walls are modeled similarly, but the curvature of the chamber wall surface is neglected, as the chamber radius is significantly larger than the radius of each body.

The model parameters include the physical and mechanical properties of the grinding body material and the chamber, as well as coefficients characterizing their contact interactions. These coefficients include the restitution coefficient (e_R), the static friction coefficient (µ_S), and the rolling friction coefficient (µ_R). While the physical and mechanical properties of most structural materials are available as reference data, determining the coefficients for contact interactions is an independent experimental task, as addressed in studies [14–16]. It should be noted that these coefficients may depend on factors such as the size and shape regularity (deviation from spherical shape) of the grinding bodies, as well as the surface roughness of the grinding bodies and the chamber. Thus, their values require refinement, which in this study was performed by fitting the model to experimental data.

As an initial approximation, based on recommendations in [17; 18], the following values were used: e_R = 0.85, µ_S = 0.45 and µ_R = 0.02. A series of numerical simulations replicating the experimental conditions was conducted, varying the contact interaction coefficients. The agreement between experimental and simulated results was evaluated based on the alignment of grinding body position patterns (instantaneous image structures) in the working chamber. Model validation was performed by comparing the areas of experimental and simulated structures of grinding bodies for eight positions of the working chamber under steady-state operation of the planetary mill. The fitting results were deemed satisfactory if the discrepancy (Δ) between experimental and simulated data did not exceed 15 % for the same values of the contact interaction coefficients.

Results and discussion

Table 1 presents typical instantaneous images of grinding bodies obtained experimentally (column “Experiment”) and from the simulated results (column “Simulation”) for various speed ratios of the working chamber to the sun wheel. Additionally, Table 1 shows images of the areas of experimental and simulated structures of the multiparticle system (column “Comparison”). Finally, Table 1 includes numerical data averaged over 8 positions of the working chamber, showing discrepancies in these areas (Δ), which represent the error of the developed model and characterize its adequacy.

Table 1. Comparison of experimental and simulated results K = w/W Experiment Simulation Comparison Δ, % 1.0 12.4 1.2 11.9 1.5 9.1 2.0 12.2

Analysis of the results presented in Table 1 indicates reasonable agreement between the experimental and simulated data, with discrepancies not exceeding 13 %. The fitting parameters were consistent across different speed ratios of the working chamber to the sun wheel. The values of the coefficients (fitting parameters) characterizing contact interactions were as follows: e_R = 0.75, µ_S = 0.21 and µ_R = 0.023. It is noteworthy that while the values of e_R and µ_R were closely aligned with or matched those used in modeling in studies [19; 20], the value of µ_S deviated significantly, exceeding a threefold difference. Nevertheless, µ_S has a substantial impact not only on the motion pattern of the grinding bodies [10] but also on the quantitative energy-force characteristics of collisions, which largely determine their accuracy. Thus, the developed model is adequate and can be used to study the effect of the gear ratio on the motion pattern of grinding bodies during high-energy ball milling and the energy-force parameters of the processing.

Using the developed model, the effect of the gear ratio on the motion pattern of grinding bodies in the working chamber was studied. The analysis of the modeling results shows that changing K from 1.0 to 1.5 has almost no effect on the kinematics of grinding body motion. In contrast, a significant change in the motion pattern is observed when K increases to 2.0. In the first case (K = 1.0÷1.5), the motion pattern is characterized by the cyclic rolling of the grinding bodies from the first row to the second row. Material processing in this mode occurs either by abrasion between the chamber wall and the grinding bodies or by collisions between grinding bodies during rolling. In the second case (K = 2.0), some grinding bodies move freely relative to the center of the working chamber. This results in three-row rolling, where two or more grinding bodies simultaneously jump to the second row, forming a third row (see Table 1). In this case, in addition to rolling, a partial mode of free flight is realized, where some grinding bodies detach from the chamber wall and are ejected into the free space of the working chamber, flying freely until colliding with another grinding body or the chamber wall. This mode is characterized by the most intense collisions. However, the number of collisions appears to decrease compared to the rolling mode.

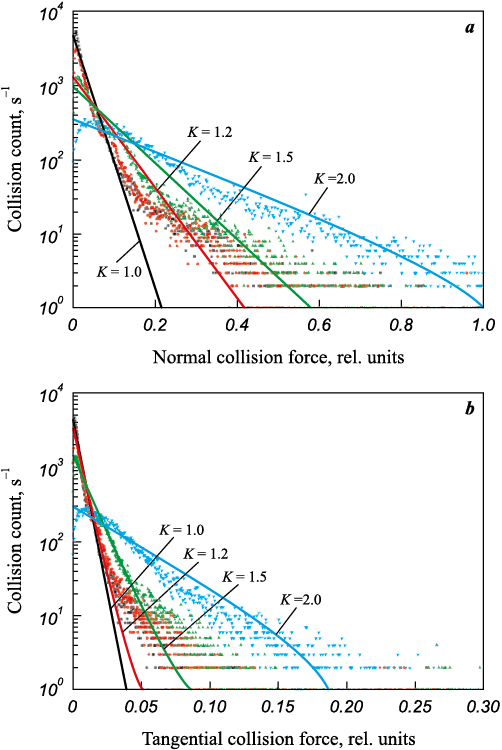
Estimates of the effect of the gear ratio on the force characteristics of contact interactions between grinding bodies and between grinding bodies and the chamber walls were also obtained. Fig. 2 presents normalized calculated data on the distribution of collision counts by compression force and shear force for different gear ratios.

It can be observed that an increase in the gear ratio contributes to the growth of the normal collision force (see Fig. 2, a). Specifically, changing K from 1 to 2 results in a ~5-fold increase in the maximum normal collision force. A significant differentiation in collision forces is also evident. For instance, if the total number of collisions is conditionally divided based on force into low-intensity (F < 0.01), medium-intensity (0.01 < F < 0.1), and high-intensity (F > 0.1), and their distribution is compared for different gear ratios (see Table 2), it becomes clear that at K = 1.0÷1.5, the majority of collisions are medium-intensity. In this range of K, the share of medium-intensity collisions increases by no more than 6 %.

Simultaneously, a redistribution of collision intensity occurs. For example, at K = 1.0, 32.5 % of collisions are low-intensity, and only 5.6 % are high-intensity. At K = 1.5, the proportion of low-intensity collisions decreases to 12.1 %, while high-intensity collisions increase to 20.1 %. However, as K increases to 2.0, with the corresponding change in the motion pattern of grinding bodies, the proportion of medium-intensity collisions decreases to 42.3 %. Conversely, the share of high-intensity collisions increases to 55.3 %, although their absolute number significantly declines. A qualitatively similar pattern was observed for tangential forces (see Fig. 2, b). It is important to note that at K = 1.0÷1.5, most collisions are medium-intensity. Assuming that these forces are sufficient to create the required field of mechanical stresses, the activation processing of material particles may be equally effective at K = 1.0 and 1.5. In contrast, processing at K = 2.0, despite the predominance of high-intensity collisions, might be less effective due to the reduced number of such collisions. This suggests that the K = 2.0 regime is more suitable for processing large particles that require greater forces for deformation and fragmentation.

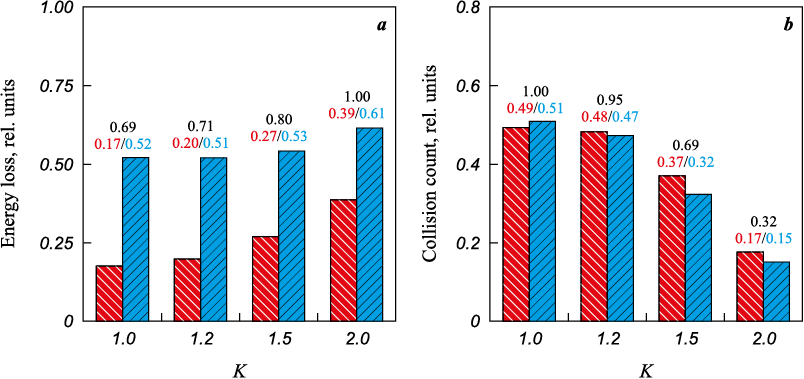
Fig. 3 presents normalized data characterizing the total energy loss during “body–body” and “body–chamber” collisions at different gear ratios, along with the changes in the number of collisions.

Analysis of the graphical dependencies presented shows that as the gear ratio K increases from 1.0 to 2.0, the total energy loss during “body–body” collisions increases by approximately 30 % (see Fig. 3, a). However, the energy loss during “body–chamber” collisions remains nearly unchanged for gear ratios K from 1.0 to 1.5, and increases by only ~13 % for K = 2.0. This indicates that the increase in total energy loss during collisions is primarily due to changes (increases) in energy loss during “body–body” collision pairs.

The number of collisions decreases predictably with an increase in the gear ratio (see Fig. 3, b). While the collision count decreases slightly for K = 1.0 and 1.2, it drops significantly at K = 1.5 (by ~1.5 times) and even further at K = 2.0 (by ~3.1 times). This reduction in collision count can decrease the likelihood of grinding bodies contacting the processed material, thereby reducing the processing efficiency. Thus, an increase in the gear ratio leads to a substantial reduction in the number of collisions while simultaneously increasing the specific energy loss per collision. This compensates for the reduction in collision count and results in a net increase in total energy loss. Interestingly, for processing mixtures of micrometer-sized particles with a high ratio of grinding body mass to material mass, the particles tend to accumulate near the chamber wall due to their ability to pass through voids between grinding bodies [19]. Consequently, despite the increase in total energy loss caused by higher K, the use of K = 2.0 may be less effective than lower K values, as “body–body” collisions do not contribute to material processing, and the number of “body–chamber” collisions, despite their increased intensity, decreases significantly. The efficiency of powder mixture processing at higher K values could potentially be improved by using a lower grinding body-to-material mass ratio, where material particles would be distributed not only near the chamber walls but also around its center. This would make better use of “body–body” collisions. Another rational application of the K = 2.0 processing regime is for large particles of millimeter-scale size, where higher forces are required for particle deformation, such as in the processing of granular or chip materials.

Conclusion

A model of grinding body motion in the “Activator-2S” planetary mill has been developed, numerically implemented, and validated. The model parameters ensuring its adequacy were determined by comparing experimental and calculated data. Analysis of the model revealed that increasing the gear ratio K from 1.0 to 2.0 decreases the proportion of grinding bodies with limited mobility and transitions their motion from rolling to a combination of rolling and free flight. This leads to an increase in the force characteristics of grinding body collisions while simultaneously reducing their count. Despite significant differentiation in collision forces, the share of medium-intensity collisions remains nearly unchanged for K = 1.0÷1.5 but decreases with a further increase in K to 2.0, resulting in a higher proportion of high-intensity collisions. Total energy loss during collisions increases by ~30 % as K changes from 1.0 to 2.0. However, energy loss during “body–chamber” collisions remains unchanged for K = 1.0÷1.5, and the increase in total energy loss is primarily due to higher energy losses during “body–body” collisions. Based on the observed effects of the gear ratio on collision patterns and energy-force characteristics of mechanical processing, the K = 1.0÷1.5 regime can be recommended for the mechanical processing of micron-sized particles with a high grinding body-to-material mass ratio. The K = 2.0 regime appears more suitable for the mechanical processing of larger particles when fragmentation of mixture components is required. The developed model can be applied to evaluate the energy-force characteristics of processing in planetary mills during the technology development stage.