Перейти к:
Особенности метода секущих, используемого для определения размера зерна в сплавах WC–Co
https://doi.org/10.17073/1997-308X-2024-3-28-37
Аннотация
На ряде сплавов WC–Co с различной шириной распределения зерен WC по размерам проведены измерения средних размеров зерен методом секущих (L) и планиметрическим методом (dдж ), а также эквивалентных диаметров (dэкв ) и средних хорд (dх ) на всех зернах и отдельно на зернах, лежащих на секущих. Установлено, что как значения средних размеров, так и распределения по размерам зерен, лежащих на секущих, и всех зерен не совпадают. Это обусловлено правилом проведения секущих в методе секущих и связанным с ним «затенением» мелких зерен крупными. Показано, что отношение средних размеров всех зерен к средним размерам зерен на линиях можно описать с использованием «теневой» функции S, зависящей от коэффициента вариации (cv ) распределения зерен WC по размерам, в виде d в/d л = 1 – S. Экспериментальные соотношения между средним эквивалентным диаметром dэкв и средним размером зерна по методу секущих L описываются выражением dэкв /L = 1,4(1 – S), а соотношения между средним размером зерна dдж и L – выражением dдж /L = 1,4(1 – S)\(\sqrt {1 + c_{\rm{v}}^2} \). Анализ распределений зерен по величине эквивалентных диаметров и средних хорд показал, что они в одинаковой степени описывают распределение зерен сплава по размерам. Распределение случайных хорд по длине, получаемое в методе секущих, не соответствует распределению зерен сплава по размерам из-за теневого эффекта и из-за того, что распределение длин случайных хорд всегда шире распределения средних хорд зерен. Показано, что распределение длин случайных хорд является сверткой функции распределения зерен по размерам и функцией, связанной с формой зерен.
Ключевые слова
Для цитирования:
Песин В.А., Васильева М.В., Осмаков А.С. Особенности метода секущих, используемого для определения размера зерна в сплавах WC–Co. Известия вузов. Порошковая металлургия и функциональные покрытия. 2024;18(3):28-37. https://doi.org/10.17073/1997-308X-2024-3-28-37
For citation:
Pesin V.A., Vasilyeva M.V., Osmakov A.S. Features of the linear intercept method used for measuring the grain size in WC–Co hardmetals. Powder Metallurgy аnd Functional Coatings (Izvestiya Vuzov. Poroshkovaya Metallurgiya i Funktsional'nye Pokrytiya). 2024;18(3):28-37. https://doi.org/10.17073/1997-308X-2024-3-28-37
Введение
Одними из основных параметров микроструктуры металлов и сплавов, определяющих их механические и физические свойства, являются размер зерна и распределение зерен материала по размерам [1–6]. В используемых методах измерения размера зерна под его размером понимаются различные характеристики, что вносит определенные сложности в сопоставление результатов работ разных авторов.
Исторически метод секущих [7] является первым методом для оценки размеров зерна в металлах и сплавах, в том числе твердых сплавах. Несмотря на развитие методов анализа изображений, он до сих пор применяется наиболее часто. Согласно методу секущих, на изображении микроструктуры сплава проводятся серии параллельных линий (секущих) и измеряются длины отрезков (случайных хорд), пересекающих каждое зерно, попавшее на одну из этих линий. При этом одно и то же зерно не должно пересекаться несколько раз. За средний размер зерна сплава принимается среднее арифметическое значение длин этих хорд, которое будет далее обозначаться как L. В ряде работ распределение длин случайных хорд используется в качестве распределения зерен по размерам [4; 8–12].
Вторым по времени появления методом оценки размеров зерна является планиметрический метод Джеффриса [13], в котором средняя площадь зерна определяется путем деления площади сечения шлифа (снимка) на количество зерен, находящихся в нем. Затем эта площадь пересчитывается в диаметр круга той же площади, называемый в литературе диаметром эквивалентного круга и обозначаемый в нашей работе dдж . Для двухфазных сплавов площадь сечения шлифа пересчитывают пропорционально объемному содержанию анализируемой фазы. С развитием компьютерных методов анализа изображений появилась возможность измерений различных размерных характеристик индивидуальных зерен, в том числе их площади. Поэтому средняя площадь зерна теперь определяется простым усреднением площадей отдельных зерен. Этот способ используется при различных модельных расчетах [14–16]. В ряде работ за размер отдельного зерна принимается эквивалентный диаметр круга (dэкв ) [6; 17; 18], рассчитываемый из площади отдельного зерна, или средняя хорда (dх ) [19]. Определение индивидуальных размеров зерен позволяет строить их распределение по размерам, что дает более полную информацию о зерновом составе материала.
Сопоставление размеров зерен, полученных различными способами, проводилось в ряде работ. Для зерен сферической формы получено соотношение между dэкв и dх [9]. В работе [15] экспериментально для ряда сплавов WC–Co независимо определялись значения L и dдж . Величина отношения dдж /L изменялась от 1,10 до 1,40 со средним значением 1,15. В этой же работе, а также в работах [14; 16] определялась величина этого отношения на модельных структурах. Для этого на кристаллах различной формы проводились произвольные сечения, а на этих сечениях – случайные хорды. Затем площади этих сечений и длины всех хорд усреднялись, и по ним определяли значения dдж , L и dдж /L. В результате были получены значения dдж /L, равные 1,74 [15] и 1,35–1,75 [16].
Эти результаты существенно отличаются от экспериментально полученных отношений. Сами авторы [15] отмечают это несоответствие, но объяснения ему не дают. Возможной причиной такого расхождения может являться то, что средний размер случайной хорды, определенный в компьютерной модели по всем зернам, может не совпадать с величиной L, измеренной методом секущих. В методе секущих проведенные линии не должны пересекать зерна дважды (ISO 4499 2(2020)). Это требование может приводить к тому, что на микрофотографиях крупные зерна могут «затенять» мелкие, которые в результате не участвуют в усреднении. Поэтому средний размер случайных хорд, определенный для всех зерен, может оказаться меньше, чем средний размер случайных хорд на секущих, и моделирование даст завышенное значение отношения dдж /L. Этот эффект «затенения» мелких зерен в дальнейшем будем называть «теневым». Существование теневого эффекта и его влияние на измеряемые значения размера зерна по методу секущих до настоящего времени в литературе не рассматривались. В связи с тем, что в ряде работ распределение зерен сплава по размерам подменяют распределением случайных хорд, отсекаемых секущими, необходимо дополнительно рассмотреть связь между этими распределениями.
Целью настоящей работы являются: количественная оценка величины теневого эффекта; определение зависимости величины теневого эффекта от характера распределения зерен WC по размерам; оценка влияния теневого эффекта на величину среднего размера зерна WC, измеряемого методом секущих; нахождение соответствия между распределением зерен WC по размерам и распределением случайных хорд по размерам в методе секущих.
Объекты и методы измерений
Проводилось сравнение размерных характеристик, измеренных по всем зернам на сечениях сплавов и по зернам, которые лежат на секущих. В качестве размерных характеристик индивидуальных зерен выбраны эквивалентный диаметр dэкв , который определенным образом связан с dдж , и средняя хорда зерна dх , связанная с L.
Для проведения исследований были отобраны 7 образцов производства компании ООО «Вириал» (г. Санкт-Петербург), представляющих собой WC–Co-сплавы с 10 мас. % Co. Среди образцов были сплавы с узким, широким и бимодальным распределениями зерен по размерам.
Для выявления границ зерен карбидной фазы проводилось травление в растворе Мураками. Микроструктура образцов исследовалась на растровом электронном микроскопе (РЭМ) MIRA 3 (Tescan, Чехия). Для анализа микрофотографий РЭМ использовалось программное обеспечение по обработке графических изображений «Fiji» (США) [20] и «ВидеоТест – Структура 5.2» (Россия).
С помощью встроенных функций этих программных пакетов были измерены следующие размерные характеристики зерен:
1. Средний размер секущей (случайной хорды) L:
\[L = \frac{1}{n}\sum {{l_i}} ,\]
где li – случайная хорда i-го зерна, пересеченного секущей.
В дальнейшем будем различать два типа размеров: с индексом «в» – размер с учетом всех зерен на микрофотографии; с индексом «л» – размер с учетом только тех зерен, которые пересечены секущими.
2. Эквивалентный диаметр Джеффриса \(d_{{\rm{дж}}}^{{\rm{в}}{\rm{, л}}}\):
\[d_{{\rm{дж}}}^{{\rm{в}}{\rm{, л}}} = \sqrt {\frac{4}{\pi }\bar A} ,\]
где \(\bar A = \sum {\frac{{A_i^{{\rm{в}}{\rm{, л}}}}}{n}} ,\) \(A_i^{{\rm{в}}{\rm{, л}}}\) площадь i-го зерна.
3. Средний эквивалентный диаметр \(d_{{\rm{экв}}}^{{\rm{в}}{\rm{, л}}}\):
\[d_{{\rm{экв}}}^{{\rm{в}}{\rm{, л}}} = \frac{1}{n}\sum {d_{{\rm{экв}}{\rm{, }}i}^{{\rm{в}}{\rm{, л}}}} ,\]
где \(d_{{\rm{экв}}{\rm{, }}i}^{{\rm{в}}{\rm{, л}}} = \sqrt {\frac{4}{\pi }A_i^{{\rm{в}}{\rm{, л}}}} \) – эквивалентный диаметр индивидуального зерна.
4. Средняя хорда \(d_{\rm{х}}^{{\rm{в}}{\rm{, л}}}\):
\[d_{\rm{х}}^{{\rm{в}}{\rm{, л}}} = \frac{1}{n}\sum {d_{{\rm{х}}{\rm{, }}i}^{{\rm{в}}{\rm{, л}}}} ,\]
где \(d_{{\rm{х}}{\rm{, }}i}^{{\rm{в}}{\rm{, л}}}\) (i – номер зерна) – средняя хорда зерна, определяемая как среднее значение из всех хорд, пересекающих зерно параллельно секущим.
Общее количество зерен на микрофотографиях для каждого сплава составляло порядка 2000–3000, а количество зерен, пересеченных секущими, – более 1000. Для каждого среднего размера зерна определялось значение стандартного отклонения и коэффициента вариации (cv ).
Экспериментальные результаты
Экспериментальные результаты измерений соответствующих средних размеров зерен с коэффициентами вариации (cv ) всех исследованных сплавов представлены в табл. 1.
Таблица 1. Измеренные размерные параметры
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
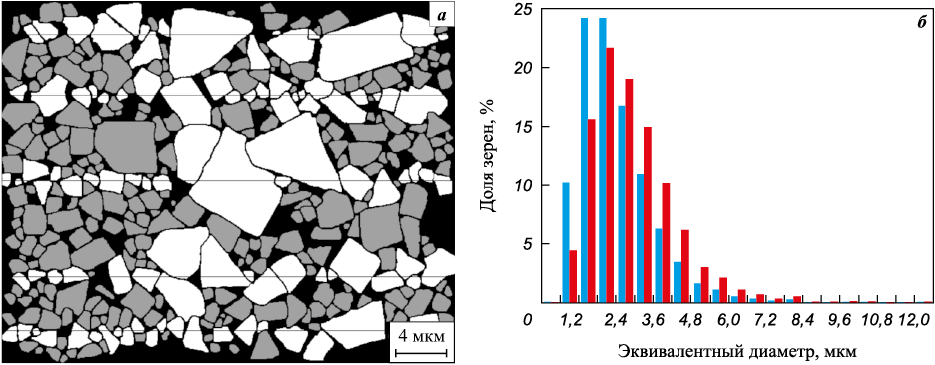
Из табл. 1 видно, что во всех случаях средние размеры зерен, которые пересекались секущими, больше, чем средние размеры для всей совокупности измеренных зерен данного сплава. Подобное проявление теневого эффекта связано с уменьшением доли мелкой фракции и, соответственно, увеличением доли крупной в распределении зерен по размерам. На рис. 1, а представлен фрагмент одного из обработанных в «Fiji» изображений для образца 2, на котором наглядно показано возникновение теневого эффекта, а на рис. 1, б демонстрируется изменение распределений зерен по величине эквивалентного диаметра для образца 3 с относительно узким распределением за счет теневого эффекта. Аналогичные результаты получаются и для величины средней хорды отдельных зерен. Таким образом, при определении среднего размера зерна методом секущих требование стандарта приводит к изменению исходных средних размеров и всего распределения зерен по размерам.
Рис. 1. Демонстрация теневого эффекта на примере фрагмента одного из обработанных |
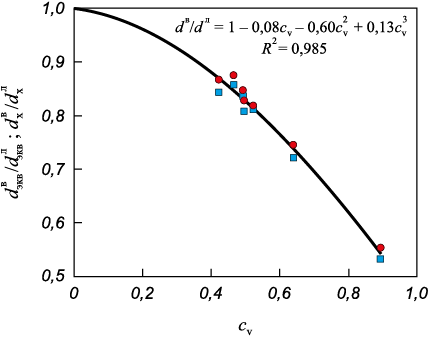
Для количественной оценки величины теневого эффекта были рассмотрены отношения средних размеров всех зерен к средним размерам зерен на секущих \(d_{{\rm{экв}}}^{\rm{в}}/d_{{\rm{экв}}}^{\rm{л}}\) и \(d_{{\rm{х}}}^{\rm{в}}/d_{{\rm{х}}}^{\rm{л}}\), а также их зависимость от величины коэффициентов вариации cv . Экспериментальные результаты представлены на рис. 2.
Рис. 2. Зависимости \(d_{{\rm{экв}}}^{\rm{в}}/d_{{\rm{экв}}}^{\rm{л}}\) и \(d_{{\rm{х}}}^{\rm{в}}/d_{{\rm{х}}}^{\rm{л}}\) от cv |
Так как для монодисперсного состава теневой эффект отсутствует, линия тренда проводилась через точку (0; 1). Как видно из рис. 2, экспериментальные данные хорошо описываются выражением
| \[{d^{\rm{в}}}/{d^{\rm{л}}} = 1 - 0,08{c_{\rm{v}}} - 0,60c_{\rm{v}}^2 + 0,13c_{\rm{v}}^3,\] | (1) |
или
| \[{d^{\rm{в}}}/{d^{\rm{л}}} = 1 - S,\] | (2) |
где «теневая» функция
| \[S = 0,08{c_{\rm{v}}} + 0,60c_{\rm{v}}^2 - 0,13c_{\rm{v}}^3,\] | (3) |
Интуитивно предполагается, что при достаточно большом количестве зерен, которые пересекаются секущими, средний размер таких случайных хорд (L) равен величине средней хорды для всех зерен (\(d_{\rm{х}}^{\rm{в}}\)). На этом предположении основывалась процедура моделирования в работах [14–16], и оно справедливо при отсутствии теневого эффекта. Однако из-за влияния теневого эффекта размер L должен совпадать с величиной средней хорды для зерен на секущих \(d_{\rm{х}}^{\rm{л}}\). И действительно, для всех сплавов получено соотношение L/\(d_{\rm{х}}^{\rm{л}}\) = 1,00 ± 0,03. Соответственно, с учетом (2) получаем
| \[L = \frac{{d_{\rm{х}}^{\rm{в}}}}{{1 - S}}.\] | (4) |
При определении зависимости \(d_{{\rm{экв}}}^{\rm{в}}\) /L от теневой функции S необходимо определить соотношение между усредненными значениями \(d_{{\rm{экв}}}^{\rm{в}}\) и \(d_{{\rm{х}}}^{\rm{в}}\). Величина отношения \(d_{{\rm{экв}}}^{{\rm{в}}{\rm{, л}}}/d_{\rm{х}}^{{\rm{в}}{\rm{, л}}}\) не зависит от вида распределения зерен сплава по размерам и определяется только формой зерен. В дальнейшем величина этого отношения будет называться коэффициентом формы Kф . Для зерен круглой формы отношение диаметра к средней хорде равно 4/π ≈ 1,27. Для зерен прямоугольной формы с учетом усреднения по ориентациям Kф ≈ 1,36, для трапециевидной – Kф ≈ 1,39, для треугольной – Kф = 1,60÷1,70 в зависимости от углов треугольника. Для всех исследованных сплавов, независимо от того, по каким зернам проводилось усреднение (по всем зернам или по зернам на линиях), было получено соотношение \(d_{{\rm{экв}}}^{{\rm{в}}{\rm{, л}}}/d_{\rm{х}}^{{\rm{в}}{\rm{, л}}}\) = 1,41 ± 0,03. Поэтому с учетом многообразия форм сечений зерен сплавов WC–Co величина Kф ≈ 1,4 представляется достаточно реалистичной. В дальнейшем будем полагать, что
| \[d_{{\rm{экв}}}^{{\rm{в}}{\rm{, л}}} = 1,4d_{\rm{х}}^{{\rm{в}}{\rm{, л}}}.\] | (5) |
Используя (4) и (5), получаем следующую зависимость:
| \[d_{{\rm{экв}}}^{\rm{в}}/L = 1,4(1 - S).\] | (6) |
Для расширения анализируемого диапазона изменений ширины распределений зерен по размерам на микрофотографиях образца 3 были выделены зерна с индивидуальными размерами \(d_{{\rm{экв}}}^{\rm{л}}\) в трех узких интервалах: 1,5 ± 0,06, 2,5 ± 0,06 и 3,1 ± 0,06 мкм (аналог δ-функции) и измерены соответствующие значения \(d_{{\rm{х}}}^{\rm{л}}\) и L. В табл. 2 представлены полученные результаты для этих узких интервалов.
Таблица 2. Измеренные размерные параметры (мкм/отн.ед.)
|
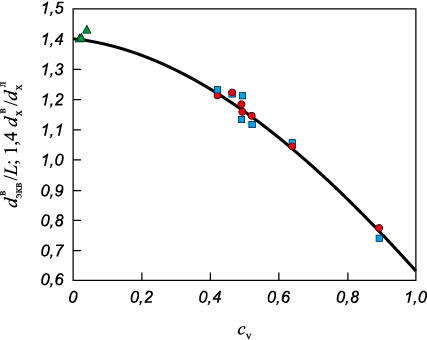
На рис. 3 показаны экспериментальные значения \(d_{{\rm{экв}}}^{\rm{в}}\)/L и \(1,4d_{\rm{х}}^{\rm{в}}/d_{\rm{х}}^{\rm{л}}\) для исследованных сплавов в зависимости от ширины распределения зерен WC по размерам, а также расчетная кривая по уравнению (6). Как видно из рис. 3, выражение (6) хорошо описывает экспериментальные данные.
Рис. 3. Зависимости \(d_{{\rm{экв}}}^{\rm{в}}\)/L и \(1,4d_{\rm{х}}^{\rm{в}}/d_{\rm{х}}^{\rm{л}}\) от cv |
Соотношение между средними размерами dдж и dэкв может быть получено из выражения \({\sigma ^2} = \sum {\frac{{{{\left( {{d_{{\rm{экв}}{\rm{, }}i}} - {d_{{\rm{экв}}}}} \right)}^2}}}{n}}\), где σ – среднеквадратичное отклонение для dэкв . Так как \(\sum {\frac{{d_{{\rm{экв}}{\rm{, }}i}^{^2}}}{n} = d_{{\rm{дж}}}^2} ,\) то получаем \({\sigma ^2} = d_{{\rm{дж}}}^2 - d_{{\rm{экв}}}^2,\) или
| \[d_{{\rm{дж}}}^{{\rm{в}}{\rm{, л}}} = d_{{\rm{экв}}}^{{\rm{в}}{\rm{, л}}}\sqrt {1 + c_{\rm{v}}^2} .\] | (7) |
Тогда из (6) и (7) получаем следующее выражение:
| \[d_{{\rm{дж}}}^{\rm{в}}/L = 1,4(1 - S)\sqrt {1 + c_{\rm{v}}^2} .\] | (8) |
Для сплавов с иной преимущественной формой зерен уравнение (8) можно записать в более общем виде:
| \[d_{{\rm{дж}}}^{\rm{в}}/L = {K_{\rm{ф}}}(1 - S)\sqrt {1 + c_{\rm{v}}^2} .\] | (9) |
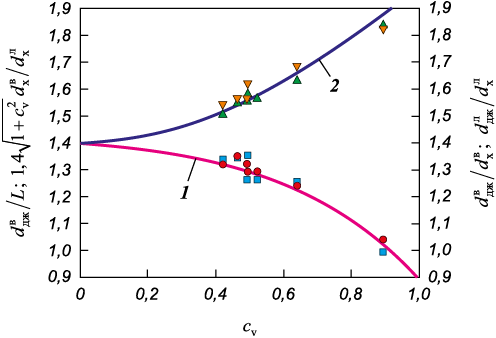
На рис. 4 для исследованных сплавов показаны экспериментальные значения \(d_{{\rm{дж}}}^{\rm{в}}/L\) и \(1,4\sqrt {1 + c_{\rm{v}}^2} d_{\rm{х}}^{\rm{в}}/d_{\rm{х}}^{\rm{л}}\) в зависимости от ширины распределения зерен WC по размерам, а также расчетная кривая по уравнению (8).
Как видно из рис. 4, уравнение (8) удовлетворительно описывает эксперимент.
Рис. 4. Зависимости \(d_{{\rm{дж}}}^{\rm{в}}/L\), \(1,4\sqrt {1 + c_{\rm{v}}^2} d_{\rm{х}}^{\rm{в}}/d_{\rm{х}}^{\rm{л}}\), \(d_{{\rm{дж}}}^{{\rm{в}}{\rm{, л}}}/d_{\rm{х}}^{{\rm{в}}{\rm{, л}}}\) от cv |
При компьютерном моделировании в работах [14–16] не учитывался теневой эффект и считалось, что L ≈ \(d_{\rm{х}}^{\rm{в}}\). В этом случае уравнение (8) принимает вид
| \[{\left( {d_{{\rm{дж}}}^{\rm{в}}/L} \right)_{{\rm{модель}}}} = 1,4\sqrt {1 + c_{\rm{v}}^2} .\] | (10) |
На рис. 4 также показана экспериментальная зависимость отношения \(d_{{\rm{дж}}}^{\rm{в}}/d_{\rm{х}}^{\rm{в}}\) от cv . Видно, что экспериментальные значения \(d_{{\rm{дж}}}^{\rm{в}}/d_{\rm{х}}^{\rm{в}}\) и \(d_{{\rm{дж}}}^{\rm{л}}/d_{\rm{х}}^{\rm{л}}\) близки к результатам расчетов [15; 16].
Помимо величины среднего размера зерна важным параметром микроструктуры является распределение зерен WC по размерам. Как видно из табл. 1, коэффициенты вариации распределений зерен сплавов по величине эквивалентных диаметров и величине средних хорд достаточно близки (расхождение в пределах 2–3 %). Распределение зерен по величине средней хорды незначительно шире из-за формы зерен. Кроме этого, было проведено сравнение распределений зерен по величине средних хорд \(d_{\rm{х}}^{\rm{в}}\) и величине \(d_{\rm{экв}}^{\rm{в}}\)/1,4 (нормировка на коэффициент 1,4 дает возможность накладывать распределения друг на друга). Наложение показало, что в пределах погрешности они совпадают. Таким образом, распределение зерен сплава по величинам \(d_{\rm{экв}}^{\rm{в}}\) и \(d_{\rm{х}}^{\rm{в}}\) могут характеризовать зерновой состав сплава в равной степени.
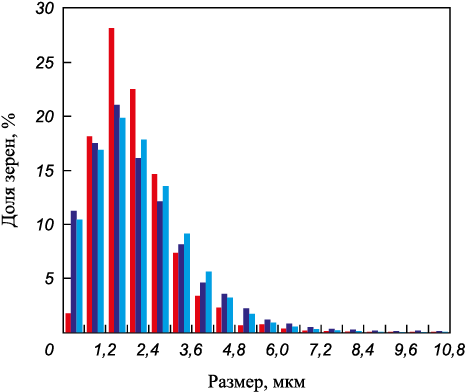
Как отмечалось ранее, распределение случайных хорд по размерам в методе секущих часто используют как характеристику зернового состава сплавов. Однако при этом необходимо учитывать, что, во-первых, распределение случайных хорд в методе секущих относится только к зернам на секущих, распределение которых отличается от распределения всех зерен сплава из-за теневого эффекта. Во-вторых, даже если имеются зерна только одного размера и формы (δ-функция), то длины случайных хорд распределяются определенным образом, и ширина этого распределения не равна нулю и определяется формой зерен. Например, если материал состоит из круглых зерен одинакового диаметра d, то средние хорды зерен также равны и, соответственно, имеют δ-распределение. При этом плотность распределения случайных хорд по размерам будет иметь вид \(f(y) = \frac{y}{d}\sqrt {{d^2} - {y^2}} ,\) y < d, где d – диаметр круга [21] с шириной распределения σ = 0,223d. Для зерен другой формы функция распределения с учетом возможных ориентаций имеет более сложный вид [22; 23]. В дальнейшем такие функции распределения мы будем называть функциями формы зерен. В результате, с математической точки зрения, распределение длин случайных хорд, получаемое в методе секущих, является сверткой функции распределения зерен по размерам на секущих и функции формы зерен. Аналогичная ситуация наблюдается во многих областях физики. При анализе распределения случайных хорд в качестве функции распределения зерен по размерам наиболее логично использовать распределение средних хорд зерен на секущих, а за функцию формы может быть принято распределение случайных хорд для узкого интервала в распределении средних хорд исследуемого сплава. В качестве иллюстрации, для зерен образца 3, лежащих на секущих, были построены распределения средних хорд, случайных хорд и расчетное распределение случайных хорд, полученное сверткой. Результаты показаны на рис. 5.
Рис. 5. Распределение зерен по величине средних хорд ( |
Сравнение функций распределения средних хорд и случайных хорд показывает, что при равных средних значениях ширина распределения случайных хорд существенно выше (коэффициенты вариации распределений различаются в 1,4–1,5 раза). В то же время распределение случайных хорд, в пределах погрешности, совпадает с полученным сверткой расчетным распределением. Это указывает на то, что даже для сплавов с относительно узкими распределениями зерен, когда теневой эффект мал, распределение случайных хорд не будет соответствовать распределению зерен сплава по размерам. Восстановление реальной функции распределения зерен сплава по размерам из распределения случайных хорд является сложной задачей и относится к классу некорректно поставленных задач по Тихонову [24].
Обсуждение результатов
Выявленные в работах [14–16] несоответствия между экспериментальными и расчетными значениями величины отношения dдж /L в сплавах WC–Co обозначили ряд проблем, связанных с методом секущих. Несмотря на широкое использование этого метода, наличия большого количества методических работ и ряда международных стандартов, как оказалось, применительно к сплавам WC–Co отсутствует понимание того, какой именно размер измеряется.
Метод секущих, так же как и планиметрический метод, разрабатывался первоначально для оценки среднего размера зерна поликристаллических металлов и сплавов, которые, как правило, имеют достаточно узкие распределения зерен по размерам. Для стандартных сплавов WC–Co характерно более широкое распределение зерен WC по размерам. Поэтому, вероятно, при практически одинаковых процедурах измерений, стандарт для металлов и сплавов ASTM E112-13(2021) и стандарт для твердых сплавов ISO 4499 2(2020) дают разные соотношения между методом линейных секущих и планиметрическим методом.
В стандарте ASTM принято соотношение \(L = \sqrt {\frac{{\pi \bar A}}{4}} ,\) которое считается точным для круглых зерен и приближенным для равноосных зерен другой формы, откуда получают \(d_{\rm{дж}}^{\rm{в}}\)/ L ≈ 1,273, или 4/π. Как ранее указывалось, эта величина равна отношению диаметра круга к его средней хорде.
В стандарте ISO, со ссылкой на [15], приводится соотношение \(L = \sqrt {\bar A} ,\) которое дает \(d_{\rm{дж}}^{\rm{в}}\)/ L ≈ 1,128, или \(\sqrt {4/\pi }\). В работе [15] экспериментальные значения отношения \(d_{\rm{дж}}^{\rm{в}}\)/ L для разных сплавов изменялись от 1,10 до 1,40 со средним 1,15, что дало основание авторам, несмотря на большой разброс результатов, принять величину отношения \(d_{\rm{дж}}^{\rm{в}}\)/ L равной 1,13 и привести ее в стандарте. Мы полагаем, что полученный в [15] разброс величины \(d_{\rm{дж}}^{\rm{в}}\)/ L связан не только с погрешностью измерений, но и с тем, что сплавы, вероятно, имели различную ширину распределения зерен WC по размерам, и простое усреднение результатов измерений \(d_{\rm{дж}}^{\rm{в}}\)/ L для разных сплавов привело, по нашему мнению, к ошибке.
Выявленная в настоящей работе зависимость среднего размера зерна WC, определяемого методом секущих, от ширины распределения зерен WC по размерам и описание этой зависимости с помощью теневой функции S позволяют устранить эту ошибку. Кроме того, имеется возможность в рамках единого подхода согласовать соотношение между результатами метода линейных секущих и планиметрического метода в стандартах ASTM E112-13(2021) и ISO 4499 2(2020). Соотношение \(d_{\rm{дж}}^{\rm{в}}\)/ L в зависимости от формы зерен и ширины распределения зерен по размерам дается уравнением (9). Для круглых и равноосных зерен коэффициент формы Kф приблизительно равен 1,27, и для относительно узких распределений (cv < 0,3) из (9) получается результат, соответствующий ASTM. Для твердых сплавов из-за разнообразия форм зерен WC коэффициент Kф приблизительно равен 1,4, а ширина распределения зерен WC может изменяться в достаточно широких пределах. Поэтому величина отношения \(d_{\rm{дж}}^{\rm{в}}\)/ L, согласно (9), может изменяться от 1,0 до 1,4 в зависимости от cv . Такой размах значений \(d_{\rm{дж}}^{\rm{в}}\)/ L полностью соответствует экспериментальным результатам [15]. Это подтверждает ошибочность простого усреднения значений \(d_{\rm{дж}}^{\rm{в}}\)/ L для сплавов с различной величиной cv и, соответственно, введение этой средней величины (1,128) в стандарт ISO 4499 2(2020). Используя выражение (8) для зависимости \(d_{\rm{дж}}^{\rm{в}}\)/ L от cv в интервале изменения cv от 0 до 1,0, получаем интегральное среднее значение 1,244.
Таким образом, применение метода секущих для определения среднего размера зерна WC в твердых сплавах реально дает еще более условную величину среднего размера, чем предполагалось ранее, в том числе и авторами. Поэтому нужно с осторожностью использовать эту величину при установлении связи между размером зерна WC и физическими свойствами сплавов. Также необходимо понимать, что распределение случайных хорд по длине в методе секущих не является распределением зерен сплава по размерам.
Выводы
1. Для ряда твердых сплавов WC–Co в результате сравнения размерных характеристик зерен WC, измеренных на всех зернах и только на секущих, показано, что условие проведения этих линий в методе секущих (ISO 4499 2) приводит к затенению крупными зернами более мелких и искажению распределения зерен WC по размерам (теневой эффект).
2. Установлено, что теневой эффект возрастает с увеличением коэффициента вариации (cv ) распределения зерен WC по размерам. Соотношение между средними размерами всех зерен и зерен на секущих может быть описано с помощью теневой функции S в виде
\[{d^{\rm{в}}}/{d^{\rm{л}}} = 1 - S,\]
где \(S = 0,08{c_{\rm{v}}} + 0,60c_{\rm{v}}^2 - 0,13c_{\rm{v}}^3.\)
3. Для исследованных твердых сплавов экспериментально получено соотношение между величинами среднего эквивалентного диаметра и средней хорды зерен WC:
dэкв ≈ 1,4dх .
4. Показано, что соотношение между средним эквивалентным диаметром, диаметром Джеффриса и величиной среднего размера зерна в методе секущих не является постоянной величиной, а зависит от величины теневого эффекта:
\[\begin{array}{c}d_{{\rm{л}}}^{\rm{экв}} = 1,4L(1 - S),\\d_{{\rm{дж}}}^{\rm{в}} = 1,4L(1 - S)\sqrt {1 + c_{\rm{v}}^2} .\end{array}\]
5. Без учета распределения зерен сплава по размерам метод секущих дает только условную оценку среднего размера и именно в таком качестве и должен рассматриваться.
6. Распределение случайных хорд по длине в методе секущих не является характеристикой распределения зерен WC по размерам.
Список литературы
1. Lee H.C., Gurland J. Hardness and deformation of cemented tungsten carbide. Materials Science and Engineering: A. 1978;33:125–133. https://doi.org/10.1016/0025-5416(78)90163-5
2. Roebuck B. Extrapolating hardness-structure property maps in WC/Co. International Journal of Refractory Metals and Hard Materials. 2006;24(1–2):101–108. https://doi.org/10.1016/j.ijrmhm.2005.04.021
3. Vornberger A., Pötschke J., Gestrich T., Herrmann M., Michaelis A. Influence of microstructure on hardness and thermal conductivity of hardmetals. International Journal of Refractory Metals and Hard Materials. 2020;88:105170. https://doi.org/10.1016/j.ijrmhm.2019.105170
4. Engqvist H., Uhrenius B. Determination of the average grain size of cemented carbides. International Journal of Refractory Metals and Hard Materials. 2003;21:31–35. https://doi.org/10.1016/S0263-4368(03)00005-2
5. Песин В.А., Осмаков А.С, Бойков С.Ю. Зависимость свойств твердых сплавов WC–Co от их состава и характеристик микроструктуры. Известия вузов. Порошковая металлургия и функциональные покрытия. 2022;16(3):37–44. https://doi.org/10.17073/1997-308X-2022-3-37-44
6. Васильева М.В., Песин В.А., Осмаков А.С., Шамшурин А.И. Исследование зависимости твердости сплавов WC–Co от характера распределения зерен WC по размерам. Заводская лаборатория. Диагностика материалов. 2023;89(2(I)):45–49. https://doi.org/10.26896/1028-6861-2023-89-2-I-45-49
7. Heyn E. Short reports from the metallurgical and metallographical laboratory of the Royal Mechanical and Technical Testing Institute of Charlottenburg. Metallographist. 1903;5:37–64.
8. Bennet E.G., Roebuck B. The metallographic measurement of hardmetal grain size. National Physical Laboratory. 2000;(22):1–52.
9. Архангельский С.И., Левин Д.М. Статистический анализ параметров и функций распределения по размерам зерен однофазных поликристаллических материалов. Заводская лаборатория. Диагностика материалов. 2020;86(4):39–45. https://doi.org/10.26896/1028-6861-2020-86-4-39-45
10. Li D., Liu Y., Ye J., Chen X., Wang L. The enhancement of the microstructure and mechanical performances of ultrafine WC–Co cemented carbides by optimizing Cr2(C,N) addition and WC particle sizes. International Journal of Refractory Metals and Hard Materials. 2021;97(1):105518. https://doi.org/10.1016/j.ijrmhm.2021.105518
11. Megret A., Vitry V., Delaunois F. High-energy ball milling of WC–10Co: Effect of the milling medium and speed on the mechanical properties. International Journal of Refractory Metals and Hard Materials. 2021;104:105774. https://doi.org/10.1016/j.ijrmhm.2021.105774
12. Chen X., Liu Y., Ye J., Wang L., Li D. Effect of rapid cooling on microstructure and properties of nanocrystalline WC–9%Co–Cr3C2–VC cemented carbide. International Journal of Refractory Metals and Hard Materials. 2022;109:105961. https://doi.org/10.1016/j.ijrmhm.2022.105961
13. Jefferies Z., Kline A.H., Zimmer E.B. The determination of the average grain size in metals. Transactions AIME. 1916;54:594–607.
14. Roebuck B. Measuring WC grain size distribution. Metal Powder Report. 1999;54(4):20–24. https://doi.org/10.1016/S0026-0657(99)80421-4
15. Roebuck B., Phatak C., Birks-Agnew I. A comparison of the linear intercept and equivalent circle methods for grain size measurement in WC/Co hardmetals. NPL Report. MATC(A). 2004;149:1–34.
16. Zeferino L.H., Buriti A.C., Monteiro S.N., da Silva A.G.P. Determination of the WC grain size in hardmetals using stereology – A critical analysis. International Journal of Refractory Metals and Hard Materials. 2008;26(4):367–371. https://doi.org/10.1016/J.IJRMHM.2007.08.011
17. Lu Z., Du J., Sun Y., Su G., Zhang C., Kong X. Effect of ultrafine WC contents on the microstructures, mechanical properties and wear resistances of regenerated coarse grained WC–10Co cemented carbides. International Journal of Refractory Metals and Hard Materials. 2021;97:105516. https://doi.org/10.1016/J.IJRMHM.2021.105516
18. Müller D., Konyashin I., Farag S., Ries B., Zaitsev A., Loginov P. WC coarsening in cemented carbides during sintering. Part I: The influence of WC grain size and grain size distribution. International Journal of Refractory Metals and Hard Materials. 2022;102:105714. https://doi.org/10.1016/j.ijrmhm.2021.105714
19. Pötschke J., Säuberlich T., Vornberger A., Meese-Marktscheffel J.A. Solid state sintered nanoscaled hardmetals and their properties. International Journal of Refractory Metals and Hard Materials. 2018;72:45–50. https://doi.org/10.1016/j.ijrmhm.2017.12.008
20. Tarrago J.M., Coureaux D., Torres Y., Wu F., Al-Dawery I.A., Llanes L. Implementation of an effective time-saving two-stage methodology for microstructural characterization of cemented carbides. International Journal of Refractory Metals and Hard Materials. 2016;55:80–86. https://doi.org/10.1016/J.IJRMHM.2015.10.006
21. Архангельский С.И., Бородихин В.М. Связь между распределениями диаметров сферических частиц и хорд их случайных сечений. Сибирский журнал индустриальной математики. 2002;5(3):27–34.
22. Агаронян Н.Г., Оганян В.К. Функции распределения длины хорды для многоугольников. Известия НАН Армении. Математика. 2005;40(4):42–57.
23. Арутюнян Г.С. Функция распределения длины хорды для правильного шестиугольника. Ученые записки ЕГУ. 2007;(1):17–24.
24. Тихонов А.Н., Арсенин В.Я. Методы решения некорректных задач. М.: Наука, 1986. 288c.
Об авторах
В. А. ПесинРоссия
Вадим Абрамович Песин – вед. специалист испытательной лаборатории № 1
Россия, 194156, г. Санкт-Петербург, пр-т Энгельса, 27Р
М. В. Васильева
Россия
Мария Владимировна Васильева – инженер испытательной лаборатории № 1
Россия, 194156, г. Санкт-Петербург, пр-т Энгельса, 27Р
А. С. Осмаков
Россия
Андрей Сергеевич Осмаков – к.т.н., начальник испытательной лаборатории № 1
Россия, 194156, г. Санкт-Петербург, пр-т Энгельса, 27Р
Рецензия
Для цитирования:
Песин В.А., Васильева М.В., Осмаков А.С. Особенности метода секущих, используемого для определения размера зерна в сплавах WC–Co. Известия вузов. Порошковая металлургия и функциональные покрытия. 2024;18(3):28-37. https://doi.org/10.17073/1997-308X-2024-3-28-37
For citation:
Pesin V.A., Vasilyeva M.V., Osmakov A.S. Features of the linear intercept method used for measuring the grain size in WC–Co hardmetals. Powder Metallurgy аnd Functional Coatings (Izvestiya Vuzov. Poroshkovaya Metallurgiya i Funktsional'nye Pokrytiya). 2024;18(3):28-37. https://doi.org/10.17073/1997-308X-2024-3-28-37