Scroll to:
Research of heat-resistant glass-ceramic coating characteristics in high-speed air plasma flow
https://doi.org/10.17073/1997-308X-2025-1-40-57
Abstract
The results of studies of thermophysical and operational characteristics of heat-resistant glass-ceramic coating on 12Cr18Ni10Ti steel in high-speed air plasma flow are presented. The coating was obtained using the slurry-firing technology. The heat treatment was carried out in air at 1400 K for 3 min. The structure of the coating is represented by a matrix based on barium silicate glass with Cr2O3 particles evenly distributed within it. The outer layer of the coating, ~3÷5 µm thick, contains many highly dispersed crystals of BaSi4O9 doped with Cr and Mo, indicating the surface glass phase crystallization. The heat capacity, thermal diffusivity and thermal conductivity of the coating in the temperature range of 293–573 K and at a pressure of 105 Pa vary in the ranges of 0.68–0.75 J/(g·K), 0.47–0.43 mm2/s and 1.198–1.222 W/(m·K), respectively. The average values of coating’s specific mass loss and entrainment rates during air plasma flow at a velocity of ~3.5 km/s and heating of the surface to 1593 K were 7.2 mg/cm2 and 25.9 mg/(cm2·h). The spectral emissivity of the coating at a wavelength of 890 nm and the rate of heterogeneous recombination of flux atoms and ions on its surface were 0.85±0.02 and 14±3 m/s. Glass phase provides effective protection of steel from high-temperature oxidation and self-healing of defects. Refractory Cr2O3 particles along with surface’s glass phase crystallization increase the resistance of the coating to erosion entrainment in the high-speed air plasma flow, its emissivity and catalyticity. The reduction of the thermal conductivity of the coating to 0.04±0.01 W/(m·K) at a temperature of 1054±10 K and a pressure of ~200 Pa is experimentally established and confirmed by numerical modelling. The explanation of the effect is presented.
Keywords
For citations:
Astapov A.N., Zhestkov B.E., Rtishcheva A.S. Research of heat-resistant glass-ceramic coating characteristics in high-speed air plasma flow. Powder Metallurgy аnd Functional Coatings (Izvestiya Vuzov. Poroshkovaya Metallurgiya i Funktsional'nye Pokrytiya). 2025;19(1):40-57. https://doi.org/10.17073/1997-308X-2025-1-40-57
Introduction
High-temperature gas corrosion of alloyed steels and nickel-based alloys is accompanied by the formation of scale on their surface, consisting of phases with variable compositions, as well as internal oxidation zones within the subscale layers. This process leads to the depletion of alloying elements, particularly Nb, Mo, and W in alloys, and decarburization in steels [1; 2]. These changes in chemical composition, in turn, result in the degradation of the mechanical properties and operational performance of the materials. The challenges become significantly more severe when alloys are exposed to high-velocity flows of oxygen-containing gases [3]. Under such conditions, oxidation processes accelerate, leading to the degradation and delamination of the oxide films formed on the surface. Additionally, the development of surface micro-relief becomes more pronounced, resulting in increased roughness, corrosion-erosion pitting, and cavity formation. These factors, in turn, contribute to greater gas turbulence in boundary regions and intensify the erosion-induced material degradation. Protecting alloys from high-temperature gas corrosion and erosion using thin-layer heat-resistant coatings is often the only viable method to maintain their high-temperature strength and functional properties. For this purpose, silicate-based glass-ceramic and glass-crystalline coatings are widely employed.
The compositions of frits (granulated glass enamels) for glass-ceramic coatings used to protect steels and nickel alloys from high-temperature gas corrosion generally contain the following main components, wt. %: 25–85 SiO2 , 20–50 BaO, 0–20 B2O3 , 0–5 Al2O3 , 0–3 MgO, 0–5 CaO [4]. To improve the adhesion properties of the formed coatings, frits include small amounts of adhesion-promoting oxides such as CoO, NiO, MnO, and MoO3 . To enhance the functional properties of the coatings (chemical resistance, erosion resistance, blackness degree, heat reflectivity, etc.), fillers such as Cr2O3 , Al2O3 , TiO2 , ZrO2 , ZrSiO4 , SiB4 , SiC, and others are introduced either through the charge during frit production or as milling additives during slurry preparation.
At present, an extensive range of resource-efficient glass-ceramic coatings has been developed, ensuring the operability of the studied materials at temperatures of 1150–1373 K for prolonged periods and up to 1473 K for short-term exposure, including in high-speed aggressive gas flows [4–6]. Among these developments, the majority are heat-resistant coatings designed for the effective protection of components and assemblies of gas turbine engines and turbopump units [1; 6–11]. However, technical solutions aimed at improving the reliability of structural elements in liquid rocket engines (for manned and cargo spacecraft, space stations, etc.) remain relatively scarce [5; 12]. There are virtually no developments in the field of protecting heat-loaded components of airframes for high-speed maneuvering aircraft and their propulsion systems [13–15]. This is primarily due to temperature-time factors that significantly limit the applicability of traditional structural materials in so-called hot structures. The challenge of ensuring short-term operability of steels and nickel alloys at temperatures of 1523–1573 K under high-speed flows (air, combustion products) remains highly relevant.
A previous invention [15] described a heat-resistant glass-ceramic coating with enhanced resistance to erosion in high-speed gas flows, providing effective protection of steels and nickel alloys during long-term operation at temperatures up to 1273 K (over 1000 h) and short-term exposure up to 1623 K (at least 15 min).
The objective of this study was to investigate the thermophysical and operational characteristics of this coating under high-speed air plasma flow conditions at surface temperatures reaching 1593 K.
1. Materials and methods
The starting components for frit production included silicon oxide (SiO2 ) powders (particle size <20 µm, purity 99.9 %), barium oxide (BaO) (<63 µm, 98 %), calcium oxide (CaO) (<63 µm, 98 %), chromium oxide (Cr2O3 ) (<10 µm, 99.9 %), aluminum oxide (Al2O3 ) (<10 µm, 98.5 %), cobalt oxide (CoO) (<45 µm, 98 %), titanium oxide (TiO2 ) (<20 µm, 99.8 %), manganese oxide (Mn2O3 ) (<20 µm, 99 %), molybdenum oxide (MoO3 ) (<3 µm, 99.9 %), and silicon tetraboride (SiB4 ) (<10 µm, 99.9 %). The components were mixed according to [15] and ground in a Pulverisette-5 planetary mill (Fritsch, Germany) using a 500 mL ZrO2 container for 180 min at a rotational speed of 400 rpm, with a mixture-to-grinding body mass ratio of 1:10. The prepared charge was placed into a 310 mL platinum crucible and melted at 1850 K for 100 min in an SVK-5163 resistance furnace (Russia) equipped with chromite-lanthanum heaters and a 3 L chamber volume. Granulation was performed by pouring the melt from the crucible into cold water.
The frit was dispersed in a high-energy ball mill “SamplePrep 8000 M-230” (Spex, USA) in a WC container with a volume of 55 mL for 60 min at a reciprocating frequency of 1080 cycles/min with short lateral movements, and a frit-to-grinding media mass ratio of 1:5. The slurry composition was prepared by mixing and wet milling the frit with kaolinite clay from the Chasov-Yar deposit, and water in the same mill for 90 min with a slurry-to-grinding media mass ratio of 1:3. The slurry's readiness was monitored by sieving it through a 63 µm mesh sieve with virtually no residue.
Austenitic stainless steel samples of grade 12Cr18Ni10Ti (wt. %: C ~ 0.12; Cr ~ 18; Ni ~ 10; Ti ~ 0.8; Fe – balance) were used as substrates, shaped as U-shaped plates with dimensions of 30×30×0.8 mm and side heights of 10 mm, as well as cylindrical samples with a diameter of 50 mm and a height of 30 mm. The sample surfaces were prepared using sandblasting with electrocorundum particles sized 50–63 µm at a pressure of 5 atm, followed by ultrasonic cleaning in isopropyl alcohol. The slurry was applied to the sample surfaces by spray coating using an airbrush with a nozzle and needle diameter of 0.8 mm. The coated layers were dried under ambient conditions with warm air (323 K) from a heater for 30 min. The firing process was conducted in a TK.4.1400.1F furnace (LLC Termokeramika, Russia) at a temperature of 1400 K for 3 min. The samples were then cooled in air at room temperature.
To determine the density and thermal diffusivity of the coating material, a compact sample with a diameter of 12.37 mm and a thickness of 1.5 mm was fabricated from the frit. The frit powder was loaded into a graphite mold and consolidated using the spark plasma sintering method on the Labox-650 system (Sinter Land Inc., Japan). The process was carried out in a vacuum at a residual pressure of 40–50 Pa, a heating rate of 80 K/min, a temperature of 973 K, a pressure of 50 MPa, and an isothermal holding time of 20 min.
The density (ρ) was determined by the hydrostatic weighing method using GR-202 analytical scales (AND, Japan) with an accuracy of 10\(^{–4}\) g. The thermal diffusivity (α) was measured using the laser flash method on the LFA447 NanoFlash device (Netzsch, Germany) in a high-purity argon atmosphere of grade 6.0. The specific heat capacity (Cp ) was determined using a differential scanning calorimeter DSC 204 F1 (Netzsch, Germany) at a heating/cooling rate of 5 K/min within the temperature range of 373–593 K under an argon flow of the same grade. The obtained data were processed using the Proteus Analysis 6 software (Netzsch, Germany). Based on the results, the thermal conductivity (λ) was calculated using the formula
| λ = αCp ρ. | (1) |
Gas-dynamic tests of the samples were conducted on an aerodynamic test stand equipped with an induction plasma torch, following the methodology described in [16]. The samples were positioned coaxially to the flow at a distance of 100 mm from the nozzle exit to the front surface of the coating. To determine the test parameters, a computational experiment was conducted, with the mathematical formulation and results provided in Section 2.3. In this study, the test conditions included a stagnation temperature T0 ~ 6000÷6500 K, a Mach number М = 4.7, a speed of 3.54 km/s, and specific heat flux values qw ~ 15÷30 W/cm2. The brightness temperature (Tb ) of the sample front surface was measured using the VS-CTT-285/E/P-2001 brightness pyrometer (LLC Videoscan, Russia) at a wavelength of 890 nm. Changes in the spectral emissivity of the samples during testing were assessed by analyzing the ratio of radiation intensities at the brightness and spectral temperatures, measured simultaneously using the USB2000+ spectrometer (Ocean Optics, USA) from the sample’s front surface. The thermodynamic (true) temperature (Tw ) of the sample's front surface was determined by recalculating the brightness temperature measured by the pyrometer, accounting for the established variation in emissivity at a wavelength of 890 nm. The mass of the samples before and after fire testing was measured using the same analytical scales as in the hydrostatic weighing method.
The heterogeneous recombination rate constant of atoms and ions (Kw ) on the active centers of the coating surface was determined based on the difference in the heat flux density between the reference and the investigated compositions, tested under identical conditions. Using parametric numerical modeling of the flow and heat transfer around the samples, the derivative dKw /dTb [16] was calculated [16]. The value of Kw for the investigated coating was determined based on the known value of Kws for the reference sample, the magnitude of dKw /dTb and the difference in brightness temperatures ΔTb of the thermally insulated investigated and reference samples, according to the following formula [16]:
| \[{K_w} = {K_{ws}} + \left( {\frac{{d{K_w}}}{{d{T_b}}}} \right)\Delta {T_b}.\] | (2) |
The product of Kw and the concentration of atoms and ions n indicates the number of atoms and ions recombining on a unit surface of the coating per second. As reference samples, samples made of fibrous thermal protection material quartz TZMK-25 with a heat-resistant enamel coating EVCH-4M1U [17] were used, for which Kws = 0.1÷0.3 m/s at temperatures of 400–1550 K.
The chemical composition of the frit powder was determined using X-ray fluorescence (XRF) analysis on an ARL OPTIM’X wavelength spectrometer (Thermo Fisher Scientific, Switzerland), which does not allow for the identification of light elements such as boron, carbon, and oxygen.
X-ray diffraction (XRD) patterns were recorded using the Bragg–Brentano geometry on an ARL X’tra diffractometer (Thermo Fisher Scientific, Switzerland) equipped with a Peltier detector and a copper anode CuKα . The measurements were performed with a step size of 0.02° at a goniometer radius of 520 mm, at a scanning speed of 0.5 °/min, within the angular range of 2θ = 10÷90°. For qualitative phase analysis, the Crystallographica Search-Match software (Oxford Cryosystems, UK) and the ICDD PDF-2 database (2010) of standard X-ray patterns were used.
Microstructural studies were conducted using an EVO-40 scanning electron microscope (SEM) (Carl Zeiss, Germany), equipped with an X-Max 50 energy-dispersive X-ray spectrometer (EDS) (Oxford Instruments, UK). Imaging was performed in both secondary and backscattered electron modes. Quantitative information on the local elemental composition of the phases was obtained using EDS at an accelerating voltage of 15 kV and a probe current of 0.5–1.5 nA. For the preparation of metallographic sections, precision equipment from Struers (Denmark) was used.
2. Results and discussion
2.1. Composition, structure, and properties
of the glass-ceramic coating
The chemical composition of the melted frit, expressed in terms of oxides (wt. %), is as follows): BaO – 34.4; SiO2 – 30.9; Cr2O3 – 22.3; CaO – 3.5; TiO2 – 2.1; CoO – 1.9; MnO – 1.9; Al2O3 – 1.6; MoO3 – 1.4. X-ray phase analysis revealed that Cr2O3 is the only crystalline phase in the frit, exhibiting rhombohedral symmetry with unit cell parameters of a = 0.49553 nm and c = 1.3581 nm. The absence of other crystalline phases, particularly SiO2 , suggests that the synthesized barium silicate glass is in an X-ray amorphous state. The composition of the resulting frit meets the concentration limits specified in the invention [15].
Fig. 1 presents the microstructures of the cross-section and surface of the glass-ceramic coating on 12Cr18Ni10Ti steel, shown in reflected and secondary electron images, characteristic X-ray radiation of elements, and a multilayer composite image created by combining electron micrographs and X-ray maps. The coating exhibits a heterogeneous structure, consisting of a barium silicate glass matrix with uniformly distributed Cr2O3 particles, with a size of no more than 10 µm. The coating thickness is 50±5 µm. The structure of the coating reveals the presence of sporadic pores and gas bubbles (Fig. 1, a, b) ranging from 4–6 µm in size (occasionally up to 10 µm). Their formation occurs during the firing process and is associated with the encapsulation of gaseous reaction products within the viscous glass phase.
Fig. 1. Microstructure of cross section (а, c–h) and surface (b) of glass-ceramic coating |
According to SEM and EDS data, the formation of the coating is accompanied by a decrease in Cr content and an increase in Fe, Ni, and Ti concentrations in the surface layers of the substrate to a depth of 3–4 µm (Table 1). The glass phase near the “substrate–coating” interface contains an increased proportion of Cr2O3 , along with small amounts of iron and nickel oxides. According to [4], the dissolution of Cr2O3 in the glass ceases once its content reaches approximately 2.5 wt. %. At a distance of 6–8 µm from the substrate interface, the glass phase acquires the characteristic chemical composition of the coating (Table 1). The presented data indicate that the enamel melt of the coating dissolves the primary scale that forms on 12Cr18Ni10Ti steel during the initial stage of firing. The formation of this scale occurs as oxygen penetrates the substrate surface through through-pores in the yet unmelted slurry layer. The dissolution of scale in the glass enamel during firing, along with the presence of adhesion-promoting oxides (CoO, MnO, and MoO3 ), contributes to improved adhesion between the coating and the substrate.
Table 1. Local chemical composition of areas on the cross section
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
The coating surface is characterized by a glassy luster and a dark green color. The outer coating layer, approximately 3–5 µm thick, contains numerous highly dispersed crystals with a high content of Ba, Cr, and Mo (Table 1), indicating surface crystallization of the glass phase. This corresponds to the upward mass transfer of Ba\(^{2+}\), Cr\(^{3+}\), and Mo\(^{6+}\) cations towards the surface, moving opposite to the concentration gradient. The crystal sizes range from 1.5–2.0 to 3–4 µm (Fig. 1, b).
According to X-ray diffraction analysis, the primary crystalline phase in the coating, as in the frit, is Cr2O3 with a rhombohedral crystal system. In addition, the presence of the BaSi4O9 phase with a trigonal structure and unit cell parameters of a = 1.1338 nm and c = 0.4548 nm was identified. The observed increase in these parameters compared to the reference values (a = 1.12469 nm and c = 0.44851 nm [18]) is likely due to the doping of the lattice with chromium and molybdenum cations, which is consistent with EDS data. Notably, the BaSi4O9 phase is known only as a high-pressure polymorph [18], and its formation through surface crystallization of the glass phase requires further investigation. The absence of other crystalline phases indirectly suggests that the matrix phase based on barium silicate glass remains in an X-ray amorphous structure.
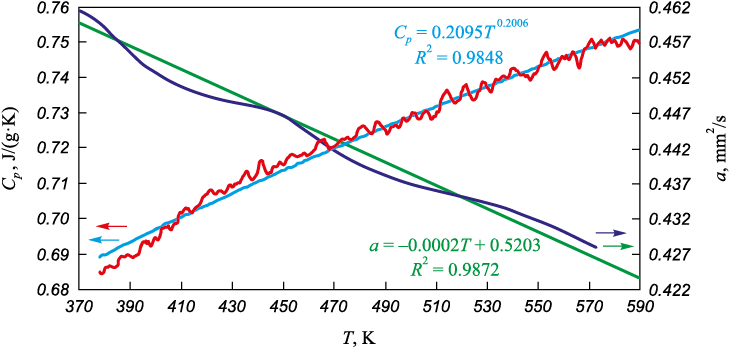
The average density of the coating, determined by the hydrostatic weighing method, was ρ = 3.813 g/сm3. Fig. 2 presents the thermophysical properties of the coating within the temperature range of 373–593 K. As the temperature increases, the heat capacity increases in a non-linear manner, while the thermal diffusivity decreases linearly. The latter behavior is typical for glass-ceramics and is attributed to increased phonon scattering with rising temperature. The coating exhibits relatively low heat capacity, with Cp = 0.68÷0.75 J/(g·K) within the temperature range of 373÷593 K. The thermal diffusivity of the coating decreases linearly from 0.47 to 0.43 mm2/s in the range of 293–573 K. Data approximation was performed using regression analysis in Microsoft Excel. The approximation results and their reliability (coefficient of determination R2) are shown in Fig. 2. The thermal conductivity of the coating, calculated using equation (1), shows minimal variation within the temperature range of 293–573 K and is λ = 1.21±0.012 W/(m·K).
Fig. 2. Temperature dependencies of heat capacity (Cp ) and thermal diffusivity (α) |
2.2. Results of gas-dynamic testing
of the glass-ceramic coating
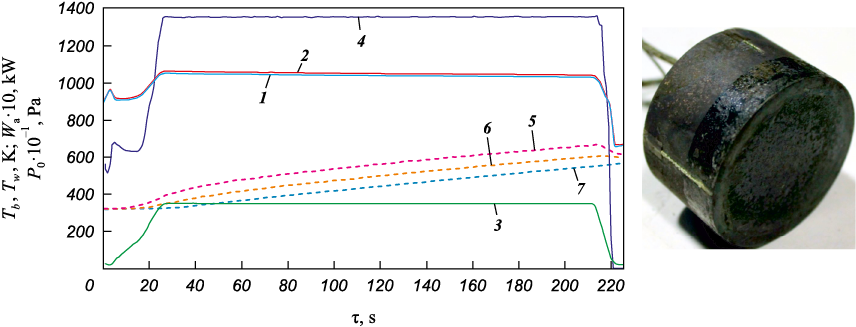
Samples made of 12Cr18Ni10Ti steel in the form of U-shaped plates with a glass-ceramic coating were sequentially installed into a cylindrical holder with a diameter of 50 mm, made of TZMK-25, flush with its end surface. A non-fired coating of the Si–TiSi2–MoSi2–TiB2–SiO2 system [19] was applied to the holder's end surface to enhance its erosive resistance and increase its emissivity. The tests were carried out under stepwise gas-dynamic heating conditions using an air plasma flow, with the front surface temperature ranging from Tw = 1193÷1593 K. Typical fire test results are shown in Fig. 3, a as profiles of the brightness temperature (Tb ) and thermodynamic temperature (Tw ) at the critical point of the front surface (curves 1 and 2), the preheater chamber pressure (P0 , curve 3) and the anode power input (Wa , curve 4). Fig. 3, b and c display photographs of the sample during testing and the coating's front surface after testing, respectively. The test series included five samples, and each fire test lasted 1000 s. The results exhibited good reproducibility, indicating the consistency of the physico-chemical processes occurring in the coating during its interaction with the air plasma, as well as the low magnitude of random errors. The average specific mass loss and erosion rate of the coating during the tests were determined to be 7.2 mg/cm2 and 25.9 mg/(cm2·h), respectively. Throughout the fire tests, the spectral emissivity of the coating at a wavelength of 890 nm remained nearly constant at ε = 0.85±0.02. The high degree of blackness of the coating is mainly attributed to the presence of numerous Cr2O3 particles within the structure, which exhibit a high emissivity (ε = 0.9). Additionally, surface crystallization contributes to enhanced radiation effects at interfacial irregularities. The stability of the emissivity value throughout the test confirms the high thermochemical stability of the coating.
Fig. 3. Results of gas-dynamic tests of a specimen made of 12Cr18Ni10Ti steel |
Fig. 4 presents the microstructures of the cross-section and surface of the glass-ceramic coating on 12Cr18Ni10Ti steel after the fire test, shown as secondary electron images, characteristic X-ray radiation element maps, and a multilayer composite image.
Fig. 4. Microstructure of cross section (а, c–h) and surface (b) of glass-ceramic coating |
The coating surface retained its gloss and dark green color. The structure of the outer layer consists of BaSi4O9 phase crystals, whose size increased to 10–15 µm (Fig. 4, b) compared to the initial state (Fig. 1, b). Their growth is likely due to recrystallization via the Ostwald mechanism.
The coating exhibits a heterogeneous, low-porosity structure, comprising a glass phase, Cr2O3 and BaSi4O9 particles, as well as spinel particles of complex composition (Fe,Co,Ni,Mn)O·(Cr,Fe,Mn,Co)2O3 , which are located within a zone extending up to 10–15 µm from the substrate interface (Fig. 4, c). The iron oxide content in the glass gradually decreases with distance from the substrate (Table 2). At the substrate-coating interface, an interface layer with a thickness of approximately 1.5–2.5 µm is formed, based on iron chromite FeO·(Cr,Fe)2O3 (Fig. 4, c, Table 2). In the surface layers of the substrate, up to a depth of 5–6 µm, a significant decrease in Cr content is observed, accompanied by an increase in Ni and Fe concentrations. In the FeO·(Cr,Fe)2O3 phase, iron is present in excess, allowing for its unrestricted diffusion through the sublayer, as evidenced by the presence of iron in the glass phase. Nevertheless, the sublayer acts as a diffusion barrier, reducing the intensity of component mass transfer. The oxidation of the substrate’s surface layer and the cations diffusing from the alloy into the coating primarily occurs due to the transport of oxidizing agents through discontinuities and defects in the coating, along the interfaces of the glassy matrix and the mentioned particles. The presence of variable-valence cations (Fe, Co, Mn, Mo) in the coating promotes oxygen absorption from the gas flow.
Table 2. Local chemical composition of areas on the cross section
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
According to X-ray diffraction analysis, the main crystalline phases in the coating after testing, as in the initial state, are Cr2O3 with a rhombohedral crystal system and BaSi4O9 with a trigonal structure. Additionally, a small amount of Fe3O4 (magnetite) phase in an orthorhombic modification with unit cell parameters a = 0.5912 nm, b = 0.5945 nm, and c = 0.8388 nm was detected, which correlates well with the SEM and EDS results. The narrowing and increased intensity of diffraction reflections from the BaSi4O9 phase indicate the gradual progression of crystallization into the coating depth. The absence of other crystalline phases indirectly suggests that the barium silicate glass matrix phase retains its X-ray amorphous state.
Based on the results of the conducted tests and the presented research data, it can be concluded that the protective properties of the coating remain intact. The glass phase effectively shields the substrate from high-temperature oxidation and facilitates self-healing of defects. The presence of refractory Cr2O3 particles (melting point Tm = 2708 K), together with the surface crystallization of the glass phase, enhances the coating's resistance to erosion in high-speed gas flows and improves its emissivity.
To evaluate the thermal conductivity and catalytic activity of the coating, an additional gas-dynamic experiment was conducted using a cylindrical sample made of 12Cr18Ni10Ti steel, with a diameter of 50 mm and a height of 30 mm, serving as a calorimeter. A coating with a thickness of 120±5 was applied to the end surface of the sample. Three chromel-alumel (type K) thermocouples (TCs) were welded to the side surface of the cylinder at distances of 0.2 mm (TC1), 5.0 mm (TC2), and 14.5 mm (TC3) from the coated end. The sample was placed in a graphite holder with a diameter of 70 mm and a height of 102.5 mm, flush with its end surface, and insulated from it using a spacer made of the thermal protection material quartz TZMK-25, with a diameter of 60 mm and a height of 40 mm. A non-fired coating of the Si–TiSi2–MoSi2–TiB2–SiO2 system [19] was applied to the holder’s surface to enhance its oxidation resistance.
The typical fire test conditions for the calorimeter cylinder are presented in Fig. 5 as profiles of brightness temperature (Tb ) and thermodynamic temperature (Tw ) at the critical point of the front surface (curves 1 and 2), preheater chamber pressure (P0 , curve 3), anode power input (Wa , curve 4), and thermocouple readings (TC1, TC2, and TC3; curves 5–7). The figure also includes a photograph of the sample after 7 test cycles conducted under this mode, with a total duration of 25 min. The average values of the specific mass loss and erosion rate of the coating after 7 test cycles were determined to be 2.8 mg/cm2 and 6.7 mg/(cm2·h), respectively. The coating retained its performance characteristics.
Fig. 5. Results of gas-dynamic tests of calorimeter sample made of 12Cr18Ni10Ti steel |
The thermal conductivity of the coating was determined based on the heat flux through it and the temperature gradient. The thermodynamic surface temperature of the coating was obtained by recalculating the brightness temperature measured by a pyrometer, taking into account the established emissivity of ε = 0.85 at a wavelength of 890 nm. The temperature beneath the coating was determined from the TC1 thermocouple readings, with a correction applied based on its placement. The heat flux through the coating was calculated from the heating rate of the sample. As shown in Fig. 5, the coating demonstrates exceptionally low thermal conductivity under these conditions. The surface temperature of the coating, Tw ~ 1054±10 K, is reached within the first Δτ1 ~ 25 s from the start of the experiment and remains more than 375 K higher than the substrate temperature even after Δτ2 ~ 185 s of heating. This corresponds to a thermal conductivity value of λ = 0.04±0.01 W/(m·K) at a temperature of Tw ~ 1054 K and a pressure of P = 214.8 Pa, which is 30.25 times lower than the value measured at temperatures of 293–573 K and pressure P = 105 Pa (see Section 2.1). The results demonstrated high reproducibility in subsequent test cycles under identical conditions. To determine the operating parameters and confirm the observed reduction in thermal conductivity, a computational simulation was performed (see Section 2.3), with further analysis of the observed effect provided in Section 2.4.
A significant contribution to the heat flux under non-equilibrium exposure to air plasma may be due to the heterogeneous recombination of atoms and ions in the flow. Therefore, catalytic activity is an important property of high-temperature materials and coatings. To assess the catalytic activity of the glass-ceramic coating, a TZMK-25 cylinder with the reference heat-resistant coating EVCh-4M1U was installed alongside the steel calorimeter cylinder in the thermal conductivity measurement setup. Under identical gas-dynamic conditions, the average brightness temperature of the reference coating was 1227 K, while the effective brightness temperature of the tested coating, calculated based on the total heat flux to the steel cylinder, was 1365 K. The heterogeneous recombination rate constant of the glass-ceramic coating, calculated using equation (2), was determined to be Kw = 14±3 m/s. This categorizes the tested coating as moderately catalytic, in contrast to highly catalytic coatings and oxide films in the HfB2–SiC–HfO2–ZrO2–Y2O3 system (Kw = 23 m/s [20]), ZrO2–Y2O3 (Kw = 33 m/s [16]), and HfO2 (Kw = 32.5 m/s [16]). The relatively high Kw value of the tested coating compared to the reference coating (Kws = 0.1÷0.3 m/s) is attributed to the significant heterogeneity of its structure, characterized by the presence of numerous primary (Cr2O3 ) and secondary (BaSi4O9 ) phase particles (see Section 2.1). This structural heterogeneity increases the number of active sites on the coating surface, where recombination of atoms and ions from the plasma flow occurs.
2.3. Numerical simulation of flow around
and unsteady heating of the cylinder
To refine the conditions of the fire test, numerical simulation of the flow around and heat transfer of the calorimeter cylinder in the working section of the setup was carried out, taking into account the reaction kinetics of dissociation and exchange processes in an 8-component mixture: О2 , N2 , О, N, NO, O\(^+\), NO\(^+\), e\(^–\). The gas mixture flow was modeled based on the Navier–Stokes equations, which describe the conservation laws of mass, momentum, and energy. It was assumed that the heat flux vector q includes three components: the conductive component, governed by Fourier's law, the convective component, caused by shear stress forces, the diffusive component, described as follows:
| \[{\bf{q}} = - \lambda \nabla T + {\bf{\tau V}} + \sum\limits_{i = 1}^K {{h_1}{{\bf{I}}_i}} ,\] | (3) |
where λ is the thermal conductivity coefficient; τ is the viscous stress tensor; V is gas velocity vector; hi is the specific enthalpy of the i-th component, and Ii is the diffusion flux vector of the i-th component.
The diffusion vector was determined using Fick's law:
| \[{{\bf{I}}_i} = - \rho {D_i}\nabla {g_i},\] | (4) |
where Di is the diffusion coefficient of the i-th component, and gi is the mass fraction of the i-th component in the mixture.
The continuity equation for the i-th component in the mixture, accounting for mass sources and diffusion, is written as follows:
| \[\frac{{\partial {\rho _i}}}{{\partial t}} + {\rm{div}}\left( {{\rho _i}{\bf{V}}} \right) = - {\rm{div}}\left( {{\rho _i}{{\bf{I}}_i}} \right) + {\omega _i}.\] | (5) |
Here, ωi represents the mass formation rate of the component per unit volume due to chemical reactions:
| \[{\omega _i} = {M_i}\sum\limits_s {\left( {{{\nu ''}_{is}} - {{\nu '}_{is}}} \right)} \left[ {{k_{fs}}\prod\limits_i {{{\left( {\frac{{{\rho _i}}}{{{M_i}}}} \right)}^{{{\nu '}_{is}}}} - {k_{rs}}\prod\limits_i {{{\left( {\frac{{{\rho _i}}}{{{M_i}}}} \right)}^{{{\nu ''}_{is}}}}} } } \right],\] | (6) |
where \({\nu '_{is}}\), \({\nu ''_{is}}\) are the stoichiometric coefficients of the reactants and products in the s-th chemical reaction.
The reaction rate constants were determined using the Arrhenius equation [21], considering the kinetic scheme presented in Table 3:
| \[{k_{f(r)}} = {A_{f(r)}}{T^{{B_{f(r)}}}}\exp \left( { - \frac{{{C_{f(r)}}}}{T}} \right),\] | (7) |
where the subscripts f and r correspond to the forward and reverse reactions, respectively.
The system of equations was closed using the equation of state for the gas mixture:
| \[p = \frac{{\rho RT}}{M},{\rm{ }}M = {\left( {\sum\limits_{i = 1}^K {\frac{{{g_i}}}{{{M_i}}}} } \right)^{ - 1}}.\] | (8) |
The specific static enthalpy of the component is given by:
| \[{h_1} = \left\{ \begin{array}{l}\frac{{5RT}}{{2{M_i}}} + {h_{0i}},{\rm{ }}i = {\rm{N}},{\rm{ O}},{\rm{ }}{{\rm{O}}^ + },{\rm{ }}{e^ - };\\\frac{{7RT}}{{2{M_i}}} + {e_{iv}} + {h_{0i}},{\rm{ }}i = {{\rm{N}}_2},{\rm{ }}{{\rm{O}}_2},{\rm{ NO}},{\rm{ N}}{{\rm{O}}^ + },\end{array} \right.\] | (9) |
Here, h0i is the specific enthalpy of formation of the i-th component, and eiv is the energy associated with the vibrational degree of freedom:
| \[{e_{iv}} = \frac{{R{\Theta _i}}}{{{M_i}\left[ {\exp \left( {\frac{{{\Theta _i}}}{T}} \right) - 1} \right]}},\] | (10) |
where Θi is the characteristic vibrational temperature of the i-th component molecule.
Table 3. Kinetic model for an eight-component gas mixture
|
When calculating the thermodynamic properties of the gas mixture, it was assumed that for each chemical component, thermodynamic equilibrium exists between translational, rotational, and vibrational degrees of freedom of the molecules. The primary temperature dependencies of the gas-dynamic and thermophysical parameters for each component were taken from references [21; 22].
It is worth noting that to reduce computational time and resource consumption, a decoupled approach was used instead of a fully coupled solution for the external flow around and unsteady heating of the solid structure. The effectiveness of this approach has been confirmed in [23].
The study of the external flow around the cylinder with a glass-ceramic coating was carried out using a computational grid of the working section, consisting of approximately 0.3 million cells. Mesh refinement was applied in the near-wall regions and near the outer boundary of the shock layer. A two-dimensional axisymmetric laminar flow of the gas mixture was simulated. At the inlet of the computational domain, the total pressure was set to P0 = 4667.7 Pa. The temperature was selected to match the test conditions, ensuring that the average total temperature in the preheater chamber fell within the range of T0 ~ 6000÷6500 K. In the initial approximation, the mass fractions of oxygen and nitrogen were set as follows: g(O2 ) = 0.23, g(N2 ) = 0.77. In subsequent calculations, the mass fractions of the components were refined for greater accuracy.
The boundary conditions at the outlet of the computational domain (outlet pressure Pout ) were set to establish a steady-state flow regime. Radiative heat transfer was applied as a boundary condition on the model surface, with the surface emissivity assumed to be ε = 0.85, and the external radiation temperature set equal to the wall temperature of the working section, Tr = 300 K. The front surface of the model with the glass-ceramic coating was considered catalytic.
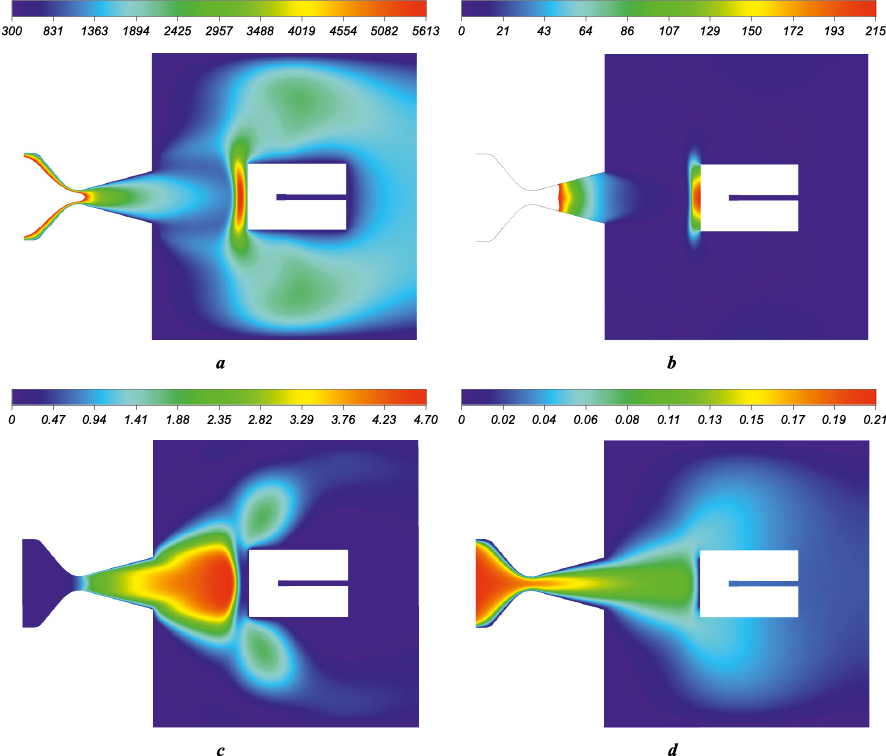
The primary calculations were conducted using the ANSYS Fluent software package (TsAGI license No. 501024), in which the described 8-component gas mixture model was implemented. The results of the flow simulation around the cylinder in the working section are shown in Fig. 6. The Mach number ahead of the shock wave reaches M = 4.7, and the plasma speed is 3.54 km/s. A curved shock wave forms at a distance of ∆x ~ 17 mm from the front surface of the cylinder, followed by a transition to subsonic flow, with a specific heat ratio γ = Cp /Cv = 1.29. The mass fractions of the main components in the incoming flow (at the nozzle exit) are as follows: g(O2 ) = 0.026; g(N2 ) = 0.727; g(O) = 0.135; g(N) = 0.023; g(NO) = 0.028; g(NO\(^+\)) = 0.061; g(O\(^+\)) = 0.325·10\(^{–3}\); g(e\(^–\)) = 1.767∙10\(^{–17}\). In front of the model, the gas temperature reaches T = 5613.2 K, and the pressure is P = 214.8 Pa.
Fig. 6. Main results of the cylinder’s external flow calculation |
The unsteady heating analysis of the cylinder with a glass-ceramic coating was conducted on a computational grid comprising ~0.9 million cells, with ~0.04 million cells assigned to the coating layer with a thickness of 125 µm.
For the calculation of convective heat transfer to the model surface, a heat transfer coefficient profile was applied:
| \[\alpha = \frac{{{q_w}}}{{{T_e} - {T_{w\max }}}},\] | (11) |
where qw and Tw max represent the heat flux density and the surface temperature, respectively, obtained from the external flow simulation. Te is the temperature at the outer boundary of the boundary layer (considered equal to the adiabatic wall temperature and determined through an additional calculation assuming qw = 0 on the model surface). The radiative heat transfer calculation was performed using the same conditions as in the external flow around simulation. The initial temperature of the entire solid structure (the cylinder with coating and thermal insulation of the lateral surfaces) was set to T0 = 291.7 K.
The thermophysical properties of the cylinder material (12Cr18Ni10Ti steel) were taken from reference data [24]. For the glass-ceramic coating, the experimentally obtained density value ρ = 3.813 g/cm3 and specific heat capacity as a function Сp = 0.2095T\(^{0.2006}\) (see Section 2.1) were used. The dependence of the thermal conductivity coefficient on the average temperature across the coating section was adjusted to match the experimentally obtained surface temperature profile and the slope of the temperature curves, which indicate the rate of temperature change at the thermocouple installation points: ∆T/∆τ ~ 1.2÷1.4 K/s (see Fig. 5). Additionally, surface temperature calculations were conducted for various values of the thermal conductivity coefficient, including λ = 1.21 W/(m·K), obtained in Section 2.1 for T = 293÷573 K at a pressure of P = 105 Pa.
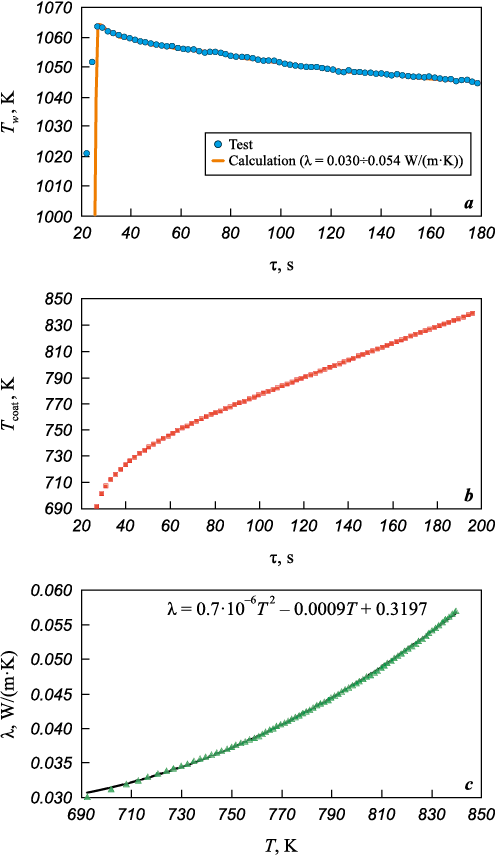
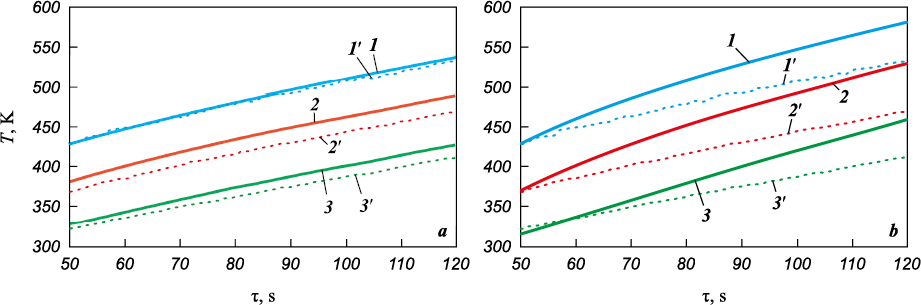
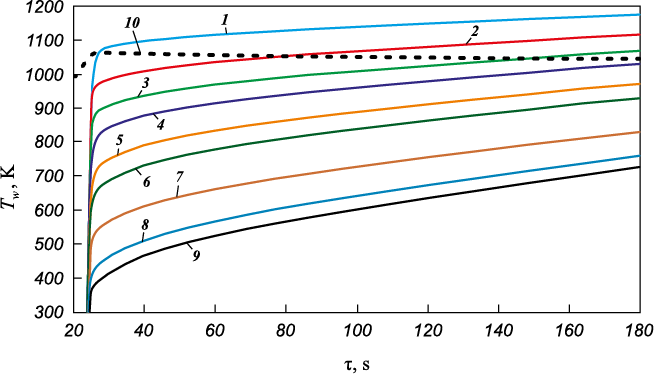
The key results of the unsteady heating simulation of the coated cylinder are presented in Figs. 7 and 8. During the test (see Fig. 5), it was found that the surface temperature of the cylinder at the front critical point initially rose sharply to Tw = 1063.5 K, which is typical for thermal insulation materials, and then gradually decreased to Tw = 1044.6 K over ∆τ ~ 185 s. Based on a series of simulations, the test-obtained surface temperature dependence at the critical point was reproduced (Fig. 7, a) by adjusting the thermal conductivity coefficient as a function of the average coating temperature across its thickness. It was shown that during the test, the surface temperature at the critical point slightly decreases, while the average temperature across the coating thickness increases to T = 840 K (Fig. 7, b). Meanwhile, the thermal conductivity coefficient increases from λ ~ 0.03 W/(m·K) at T = 690 K to λ ~ 0.057 W/(m·K) at T = 840 K (Fig. 7, c). The approximation of the computational data allowed for the establishment of the relationship λ = f1(T), presented in Fig. 7, c. The increase in thermal conductivity with temperature enables obtaining a monotonically decreasing dependence Tw = f2(τ) (Fig. 7, a). The calculated temperatures at the thermocouple installation points agree within 5 % with the test results (Fig. 8, a). The calculated values of the heat flux density at the front critical point were qw = 18.2÷18.5 W/cm2, which falls within 2 % of the test-measured values.
Fig. 7. Results of surface temperature evolution calculation Tw (а)
Fig. 8. Comparison of experimental and calculated results of temperature evolution |
Fig. 9 presents a comparison of test and calculated results for the evolution of surface temperature at the critical point of the coating for different values of the thermal conductivity coefficient. In each calculation, the thermal conductivity coefficient was assumed to be constant. The simulation results were found to be in good agreement with the test data. It was demonstrated that at λ = 1.21 W/(m·K), the surface temperature at the front critical point increased only to Tw ~ 730 K during the test, which does not align with the test results. Moreover, the rate of temperature change at the thermocouple installation points exceeded the test values by approximately 1.4 times (Fig. 8, b).
Fig. 9. Calculated and experimental cylinder-calorimeter surface temperatures evolution results |
Thus, numerical simulation of the gas-dynamic test confirmed that at low pressures (P ~ 200 Pa), a significant reduction in the thermal conductivity of the glass-ceramic coating occurs. The obtained thermal conductivity values of λ = 0.030÷0.057 W/(m·K) were observed within the temperature range T = 690÷840 K and the average value of thermal conductivity coefficient, determined during the test ∆τ ~ 185 s, was λ ~ 0.04 W/(m·K), which is in full agreement with the test-derived value (see Section 2.2).
2.4. Effect of reduced thermal conductivity
with decreasing pressure
The thermal conductivity of the glass-ceramic coating is primarily determined by atomic thermal vibrations, known as the phonon transport mechanism. A decrease in thermal conductivity occurs as the phonon mean free path is reduced due to phonon scattering at structural defects, such as impurity atoms, grain boundaries, phase interfaces, and voids, as well as interactions with other phonons. As temperature increases, phonon-phonon interactions intensify, and in combination with the highly disordered (amorphous) structure of the glass phase, this results in extremely short phonon mean free paths. When external pressure decreases, the phonon mean free path is further shortened due to the reduced propagation velocity of acoustic waves resulting from the lower density of the medium.
In the presence of structural inhomogeneities, such as pores, voids, and cracks, the thermal conductivity of dielectrics is influenced not only by the phonon mechanism but also by convective gas transport within these discontinuities. The extent of convection is strongly dependent on the distribution and geometry of the discontinuities, as well as the thermal conductivity of the enclosed gas. The convective effect diminishes with decreasing discontinuity size, reduced interconnectivity, and lower surrounding gas pressure.
The investigated coating contains voids with sizes up to ~5–10 µm (see Fig. 1). It is known [25] that at low pressures (Р < 103 Pa), when the mean free path of gas particles l is much greater than the void size L (l \( \gg \) L), the thermal conductivity of porous materials is proportional to the gas pressure, increases with rising temperature, and approaches zero as pressure decreases. This phenomenon is likely due to the fact that when (l \( \gg \) L, gas particles remain adsorbed on the surface of the voids for a long period before experiencing collisions. As pressure decreases, the number of gas particles in the voids is reduced, and an increasing fraction of them becomes adsorbed on the void surfaces, leading to a decrease in the convective component of heat transfer. At temperatures above 1200 K, radiative heat transfer in discontinuities should also be considered, as its contribution to overall thermal conductivity increases with temperature. It should be noted that in the fire tests conducted to determine the thermal conductivity of the glass-ceramic coating, the pressure at the sample surface was Р ~ 200 Pa, and the temperature Tw ~ 1050 K, satisfying the condition (l \( \gg \) L. This, combined with the reduced phonon mean free path, explains the extremely low thermal conductivity of the coating.
A threefold reduction in thermal conductivity (from 0.05 to 0.0167 W/(m·K) at 293 K) with a decrease in external pressure (from 105 to 133.3 Pa) was previously observed during tests of the highly porous quartz thermal protection material TZMK-10 [26]. The explanation of this observed effect is presented here for the first time.
The conducted studies of the glass-ceramic coating have enabled its application in thermal testing of various steel models in the TsAGI aerodynamic wind tunnels [27]. The high and stable emissivity of the coating over time enhances the accuracy of temperature measurements of models using optical methods under illumination conditions. The coating’s heat and erosion resistance slow down oxidation processes, reduce mechanical erosion, and prevent the formation of corrosion-erosion pitting and cavities on model surfaces, which further contributes to the improved accuracy of conducted studies and measurements.
Conclusion
A thin-layer heat-resistant glass-ceramic coating was obtained on 12Cr18Ni10Ti steel samples using the slurry-firing deposition method. The coating exhibits a heterogeneous structure, consisting of a barium silicate glass matrix with uniformly distributed Cr2O3 particles. In the outer layer of the coating, with a thickness of approximately 3–5 µm, numerous highly dispersed BaSi4O9 crystals doped with Cr and Mo were identified, indicating surface crystallization of the glass phase. The coating is characterized by a low density of 3.813 g/cm3 and a highly continuous structure. The heat capacity, thermal diffusivity, and thermal conductivity of the coating within the temperature range of 293–573 K and at a pressure of 105 Pa vary within the ranges of 0.68–0.75 J/(g·K), 0.47–0.43 mm2/s, and 1.198–1.222 W/(m·K), respectively.
Fire tests of the coating were conducted under conditions of aerogas-dynamic flow and non-equilibrium heating by air plasma at a speed of approximately 3.5 km/s and a specific heat flux of 15–30 W/cm2, achieving temperatures of up to 1593 K on the front surface. The average values of specific mass loss and erosion rate of the coating were 7.2 mg/cm2 and 25.9 mg/(cm2·h), respectively. The spectral emissivity of the coating at a wavelength of 890 nm and the heterogeneous recombination rate of atoms and ions on its surface were determined to be 0.85±0.02 and 14±3 m/s, respectively. The glass phase effectively protects the steel from high-temperature oxidation and facilitates self-healing of defects. The presence of refractory Cr2O3 particles, along with the surface crystallization of the glass phase, enhances the coating’s resistance to erosion in high-speed air plasma flow, its emissivity, and catalytic activity.
A reduction in the coating’s thermal conductivity to 0.04±0.01 W/(m·K) at a temperature of 1054±10 K and a pressure of ~200 Pa was experimentally established and confirmed by numerical simulation. An explanation of this effect has been provided.
References
1. Zakalashniy A.V., Denisova V.S., Kulikova O.V., Agarkov A.B. Polyfunctional heat-resistant coating for protecting corrosion-resistant steel parts. Glass and Ceramics. 2024;80:404–408. https://doi.org/10.1007/s10717-023-00623-4
2. Fu G.Y., Wei L.Q., Zhang X.M., Cui Y.B., Lv C.C., Ding J., Yu B., Ye S.F. A high-silicon anti-oxidation coating for carbon steel at high temperature. Surface and Coatings Technology. 2017;310:166–172. https://doi.org/10.1016/j.surfcoat.2016.12.084
3. Terentieva V.S., Astapov A.N., Rabinskiy L.N. State in the field of heat-resistant coatings for heat-proof nickel alloys and steels. Periodico Tche Quimica. 2019;16(33):561–572. http://dx.doi.org/10.52571/PTQ.v16.n33.2019.576_Periodico33_pgs_561_572.pdf
4. Solntsev S.S. Protective technological coatings and refractory enamels. Moscow: Lenand, 2016. 304 p. (In Russ.).
5. Aviation materials: Handbook. In 12 vol. Vol. 9. Heat-protective, thermal insulation and composite materials, high-temperature non-metallic coatings. Ed. E.N. Kablov. Moscow: VIAM, 2011. 176 p. (In Russ.).
6. Denisova V.S., Vlasova O.V., Malinina G.A. Effect of the addition of silicon tetraboride on the thermal stability of reaction cured coatings. Aviation Materials and Technologies. 2020;59(2):50–55. (In Russ.). https://doi.org/10.18577/2071-9140-2020-0-2-50-55
7. Bettridge D. Metallic article having a protective coating and a method of applying a protective coating to a metallic article: Patent 6444332 (USA). 2002.
8. Solntsev S.S., Isaeva N.V., Shvagireva V.V., Solov'eva G.A. Heat-resistant coating: Patent 2273609 (RF). 2006. (In Russ.).
9. Solov'eva G.A., Grashchenkov D.V., Isaeva N.V., Shvagireva V.V. Heat-resistant coating: Patent 2358925 (RF). 2009. (In Russ.).
10. Hazel B.T., Murphy J.A., Skoog A.J., Bojanowski B.T., Weimer M.J. Strain tolerant corrosion protecting coating and spray method of application: Patent 7754342 (USA). 2010.
11. Kablov E.N., Solntsev S.S., Rozenenkova V.A., Denisova V.S. Heat-resistant cover: Patent 2598657 (RF). 2016. (In Russ.)
12. Miller T.J., Pinera A., Brooks S.M., Appleby Jr. J.W., Leonard T.G. Turbopump with a single piece housing and a smooth enamel glass surface: Patent 2017/0082070 (USA). 2017.
13. Lima R.S., Cojocaru C.V., Moreau C., Wang Y. Method and apparatus for depositing stable crystalline phase coatings of high temperature ceramics: Patent 2014/0329021 (USA). 2014.
14. Russell J.C., White T.L., Shiflett B., Cherinet P., Wadley S., Barnhart C., Khozikov V., Nakamoto K. Nano-coating thermal barrier and method for making the same: Patent 2576864 (EP). 2018.
15. Astapov A.N., Barabanov B.N., Eremina A.I., Lifanov I.P. Method of producing heat-resistant glass-ceramic coating: Patent 2679774 (RF). 2019. (In Russ.).
16. Astapov A.N., Zhestkov B.E., Senyuev I.V., Shtapov V.V. Methodology of studying high-velocity plasma flow impact on high-temperature materials. AIP Conference Proceedings. 2023;2549(1):210009. https://doi.org/10.1063/5.0109458
17. Zhestkov B.E., Shtapov V.V. Methodology of studying materials in hypersonic plasma flow. Zavodskaya laboratoriya. Diagnostika materialov. 2016;82(12):58–65. (In Russ.).
18. Hazen R.M., Yang H., Finger L.W., Fursenko B.A. Crystal chemistry of high-pressure BaSi4O9 in the trigonal (P3) barium tetragermanate structure. American Mineralogist. 1999;84:987–989. https://doi.org/10.2138/am-1999-5-636
19. Astapov A.N. Heat-resistant non-fired repair coatings for protection of carbon-base materials. International Journal of Nanomechanics Science and Technology. 2014;5(4):267–285. https://doi.org/10.1615/NanomechanicsSciTechnolIntJ.v5.i4.20
20. Kablov E.N., Zhestkov B.E., Grashchenkov D.V., Sorokin O.Yu., Lebedeva Yu.E., Vaganova M.L. Investigation of the oxidative resistance of high-temperature coating on a SiC material under exposure to high-enthalpy flow. High Temperature. 2017;55(6):873–879. https://doi.org/10.1134/S0018151X17060086
21. Gupta R.N., Yos J.M., Thompson R.A., Lee K.-P. A review of reaction rates and thermodynamic and transport properties for the 11-species air model for chemical and thermal nonequilibrium calculations to 30 000 К. NASA Reference Publication. 1990;1232. 91 p.
22. McBride B.J., Gordon S., Reno М.A. Coefficients for calculating thermodynamic and transport properties of individual species. NASA Technical Memorandum. 1993;4513. 94 p.
23. Drozdov S.M., Rtishcheva A.S. Analysis of flow-field and heat exchange for a blunted cone at hypersonic speeds. Journal of Physics: Conference Series. 2020;1683:022030. http://doi.org/10.1088/1742-6596/1683/2/022030
24. Steel and alloy brand book: Handbook. Ed. V.G. Sorokin. Moscow: Mashinostroenie, 1989. 640 p. (In Russ.).
25. Physical quantities: Handbook. Eds. I.S. Grigor’ev, E.Z. Meilikhov. Moscow: Energoatomizdat, 1991. 1232 p. (In Russ.).
26. Shchetanov B.V. Tile material for external high-temperature thermal protective coating of the Buran orbital spacecraft. Aviation Materials and Technologies. 2013;S1:41–50. (In Russ.).
27. Rtishcheva A.S. Application of numerical modeling to determine heat flux on the surface of bodies in a thermal experiment. In: Models and methods of aerodynamics: Proceedings of the XXII International school-seminar (Sochi, 4–9 September 2022). Moscow: TsAGI, 2022. P. 70–72. (In Russ.).
About the Authors
A. N. AstapovRussian Federation
Alexey N. Astapov – Cand. Sci. (Eng.), Associate Professor of the Department of Advanced Materials and Technologies for Aerospace Application, Researcher
4 Volokolamskoe Shosse, Moscow 125993, Russia
B. E. Zhestkov
Russian Federation
Boris E. Zhestkov – Cand. Sci. (Eng.), Senior Researcher, Head of Laboratory
1 Zhukovsky Str., Zhukovsky, Moscow Region 140180, Russia
A. S. Rtishcheva
Russian Federation
Alena S. Rtishcheva – Cand. Sci. (Eng.), Associate Professor, Head of Sector
1 Zhukovsky Str., Zhukovsky, Moscow Region 140180, Russia
Review
For citations:
Astapov A.N., Zhestkov B.E., Rtishcheva A.S. Research of heat-resistant glass-ceramic coating characteristics in high-speed air plasma flow. Powder Metallurgy аnd Functional Coatings (Izvestiya Vuzov. Poroshkovaya Metallurgiya i Funktsional'nye Pokrytiya). 2025;19(1):40-57. https://doi.org/10.17073/1997-308X-2025-1-40-57
JATS XML