Optimization of powder mixing parameters for the Al–Sn–Pb system for use in selective laser melting

Introduction

The growing demand for high-performance antifriction materials in advanced engineering applications is driving the development of new metallic powder compositions designed to produce components with enhanced tribological properties [1–3]. This trend, combined with the rapid adoption of additive manufacturing technologies, imposes stricter requirements on the preparation of multicomponent powder mixtures. The extreme nonequilibrium conditions of the selective laser melting (SLM) process, characterized by intense heating (>10⁶ K/s) and cooling rates (10³–10⁸ K/s), necessitate a high degree of homogeneity in the initial powder mixture, as any inhomogeneities can lead to structural defects and anisotropy, ultimately degrading the properties of the final components [4; 5].

Aluminum alloys are among the most widely used materials across various industries due to their unique combination of strength and low density, enabling the production of lightweight yet durable machine components. The integration of aluminum alloys into 3D printing technologies further enhances their appeal by providing additional design flexibility in terms of shape and structure [6]. The Al–15Sn–5Pb (vol. %) system is a specialized alloy intended for antifriction applications, such as sliding bearings, where tin and lead act as solid lubricants, reducing wear during frictional contact [7–9]. However, the tendency of these inclusions to segregate during both powder mixing and solidification in the 3D printing process necessitates stringent control over the composition of the powder mixture to ensure their uniform distribution in the final product [10]. Additionally, the relatively low evaporation temperature of lead (1749 °C) compared to the typical process temperatures of aluminum alloy SLM (>2000 °C) requires precise energy input control to prevent selective evaporation [11].

Mixing powders with significant density differences poses a fundamental challenge [12]. In the Al–15Sn–5Pb system, where the density ratio of lead to aluminum is approximately 4.2:1.0, this issue becomes particularly pronounced. Traditional drum mixers, which operate mainly by gravitational forces, tend to promote segregation rather than effective mixing in such systems, as denser lead and tin particles naturally migrate downward. This results in localized inhomogeneities in the powder mixture, which is critical for its subsequent use in SLM [13]. One potential solution to this problem is the use of a Turbula-type mixer manufactured by Vibrotechnik (Russia), which combines rotational and translational motion in a rhythmic three-dimensional pattern. This complex motion induces intense mixing conditions that counteract gravitational effects, thereby reducing segregation driven by density differences. The powder layer periodically experiences near-weightlessness, followed by abrupt directional changes, which help prevent agglomeration.

The objective of this study was to evaluate the effectiveness of the modified Hertz–Mindlin model in predicting the quality of the resulting powder mixture composed of components with significant density variations, as well as to determine the optimal mixing parameters for the Al–15Sn–5Pb system using a Turbula-type mixer. The research focused on identifying the minimum mixing time required to achieve compositional homogeneity sufficient for the successful application of powder mixtures with large density differences in the SLM process.

Materials and methods

The experiments were conducted using aluminum (ASD-1), tin (PO-1), and lead (PS-1) powders. The powders were sieved through meshes with an upper cell size limit of 50 µm and a lower limit of 25 µm.

Analysis of several scanning electron microscopy (SEM) images revealed that the average particle size of all studied powders was 30 µm (Fig. 1), with a size distribution approximating a normal distribution. The aluminum powder particles had a spherical shape, whereas the tin and lead powders exhibited both spherical and dumbbell-like morphologies.

Additionally, powder flowability was analyzed using funnels with outlet diameters of 2.5 mm (tin, lead) and 5 mm (aluminum) according to GOST 20899–98 (ISO 4490–78). Measurements of the natural repose angle showed that its value for all three powders was approximately 30°. The flowability of the tin and lead powders did not exceed 20 s/50 g, while that of aluminum was 26 s/50 g, indicating their suitability for SLM technology.

Mixing simulations were performed using the discrete element method (DEM) with the Altair EDEM software package (Altair Engineering, USA). The particle-to-particle and particle-to-wall interactions were described by the Hertz–Mindlin model, modified according to the Johnson–Kendall–Roberts (JKR) theory [14; 15]. This contact interaction model is widely used in powder mixing simulations to account for adhesion forces [16–21]. To accelerate computational time, model scaling was applied, reducing the container size and powder mass by a factor of three.

The physical parameters of the powders used in the model are presented in Tables 1 and 2. The friction and restitution coefficients were averaged based on data from various sources [22–26]. For Sn and Pb friction pairs, the friction coefficients were taken from similar bearing steels with comparable properties.

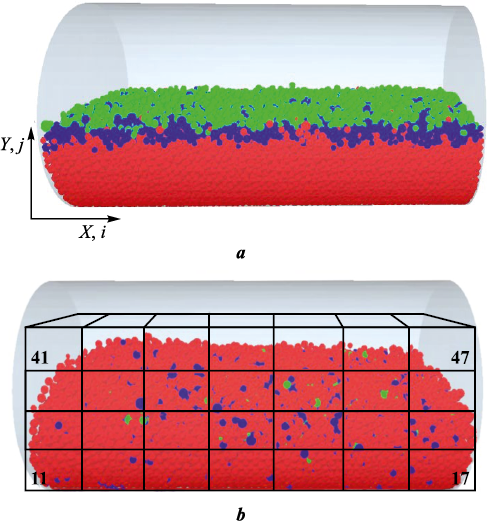
To analyze the variation in the tin and lead powder content during mixing, the container volume was conditionally divided into 28 cells, where the fraction of each metal’s particles was assessed using the formula N_ij/V_ij, where N_ij is the number of Sn and Pb particles, V_ij is the cell volume, and i and j are the cell indices along the X and Y axes, respectively (Fig. 2).

In a Turbula-type mixer, the powder mixture was blended at a container rotation speed of 30 rpm. The mixing duration varied within the range of τ = 10÷240 min. From the obtained mixtures, 10 compacts were produced by pressing, with the powder for each compact being taken from different parts of the container.

An initial analysis of the composition of the initial components in the powder mixture was performed using X-ray phase analysis with a DRON-8 diffractometer (NPP Burevestnik, Russia) in CuK_α radiation (λ = 1.5406 Å) over a 2θ range of 10–110°.

For metallographic studies, cross-sections of the compacts along their diameters were examined. The microstructural analysis of the obtained compacts, as well as the elemental composition assessment, was conducted using a LEO EVO 50 scanning electron microscope (Carl Zeiss, Germany) equipped with an energy-dispersive X-ray spectroscopy (EDS) module. The graphical analysis of SEM images of the compact cross-sections was performed using ImageJ software (National Institutes of Health, USA).

Results and discussion

Simulation

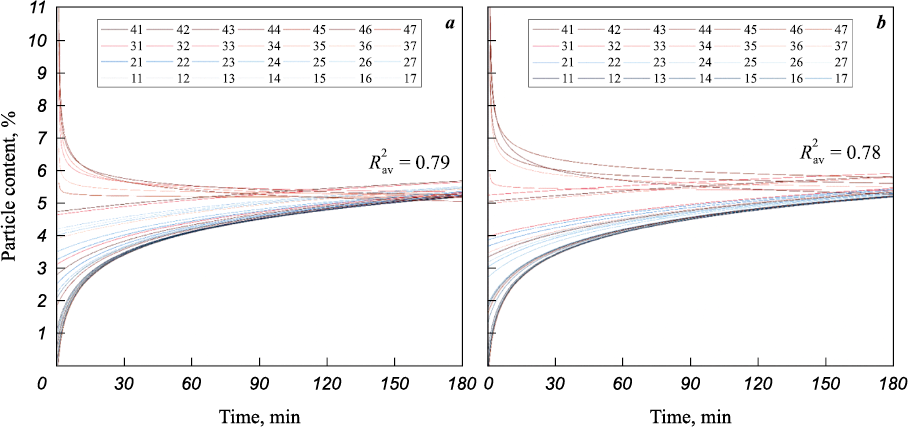
The simulation results for the number of tin and lead particles in different areas of the container over 3 h of mixing, approximated by logarithmic dependencies, are presented in Fig. 3. It was found that at a mixing duration (τ) of up to 30 min, the majority of both lead and tin particles remain predominantly in the upper layers of the powder mixture, despite the complex motion pattern of the container during the process. This may be attributed to the formation of temporary agglomerates of Sn and Pb particles, as these powders exhibit a high tendency toward adhesion due to their lower hardness and high plasticity compared to aluminum, leading to the formation of more stable contacts. As τ increases to 60 min, the dependencies of Sn and Pb particle content in different cells converge within the 4–6 % range and nearly equalize at 180 min.

Based on these results, it can be assumed that to obtain a near-homogeneous Al–15Sn–5Pb mixture, the minimum mixing time in the Turbula mixer should be 60 min at a container rotation speed of 30 rpm.

Experiment

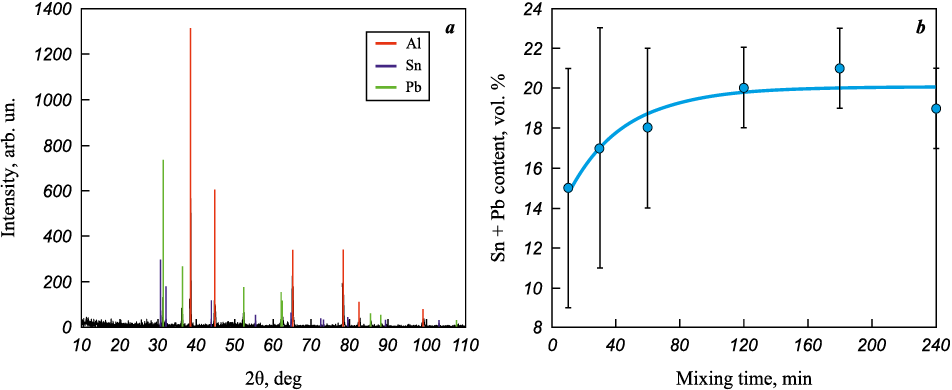
A typical diffractogram of a compact made from the Al–15Sn–5Pb mixture and the dependence of the soft-phase (Sn + Pb) content on the mixing time, calculated using the corundum number method, are presented in Fig. 4. It can be observed that at short mixing times, the soft-phase content is lower (15 vol. %), with significant variations (6 %) in its values (Fig. 4, b). These data partially confirm the simulation results, indicating the presence of soft-phase particle agglomerates. The expected tin and lead content levels in the mixture are reached after 60 min of mixing, confirming the reliability of the applied numerical model. In the 120–180 min time range, the dependence acquires a linear character, and the variation in soft-phase element content does not exceed 2 %.

The results of SEM studies, presented in Fig. 5, indicate that at short mixing times (τ = 10–60 min), an uneven distribution of soft-phase particles is observed, with large agglomerates of various shapes reaching 300 µm in size. The use of such powder mixtures in SLM would likely result in large defects due to local inhomogeneities in the initial powder distribution. At τ = 120–240 min, tin and lead become more evenly distributed across the polished section surface, and the size of soft-phase agglomerates decreases. Completely eliminating these agglomerates is not feasible due to the inherent tendency of these powders to adhere. However, at this stage, the powder mixtures can be considered suitable for SLM technology.

The EDS analysis results of the compact element composition are presented in Table 3. According to the data, even at short mixing times, the mixture contains Sn and Pb levels close to the target composition. However, due to inhomogeneous distribution within the powder volume, a significant deviation from the mean is observed in different sections of the compacts. After 60 min of mixing, these deviations are reduced by approximately a factor of two, indicating the breakdown of large agglomerates. Mixing for 120 min or longer further decreases the deviation from the average element content within different compact sections to ≈2 %, suggesting that the elements have reached a sufficiently homogeneous distribution throughout the volume.

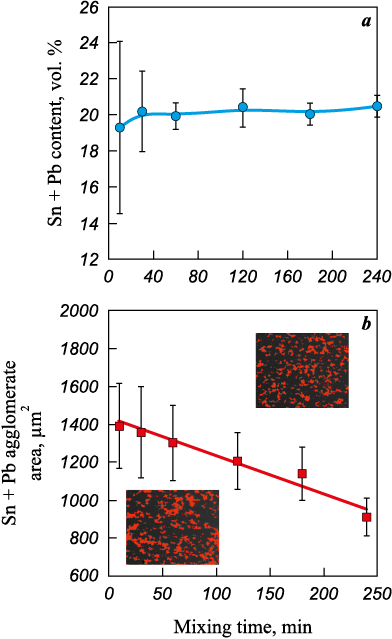
In addition to EDS analysis, graphical analysis of SEM images was conducted using ImageJ software to assess the quantity and size of soft-phase (Sn + Pb) agglomerates (Fig. 6). The fraction of lead and tin was determined based on the area occupied by these particles. For each τ value, 10 images per compact were analyzed.

The analysis revealed that the tin and lead content follows an approximately linear trend. However, at short mixing times, as observed in the EDS results, there is a high relative deviation in particle distribution within the volume (±6 %), which decreases to 1 % as τ increases. Despite the relative deviation reduction occurring as early as τ = 60 min, it is also important to consider the size of Sn and Pb agglomerates. The trend in agglomerate area reduction follows a linear downward pattern. With an increase in mixing duration, the agglomerate area decreases by approximately 35 %, from 1400 to 900 µm² at τ = 10 and 240 min, respectively. At the same time, the deviation value also decreases from 16 to 10 %, but remains relatively high. This is likely due to the formation of agglomerates within the internal volume of the powder mixture, which, lacking direct contact with the container walls, were more resistant to breakdown during mixing.

These findings indicate not only an improvement in mixture homogeneity within a relatively short period (τ = 60–120 min) but also the effectiveness of the modified Hertz–Mindlin model for simulating the mixing process in powder systems with significant density differences between their components.

Conclusions

Based on the obtained results, the following conclusions can be drawn.

1. The complex motion pattern of the Turbula mixer ensures effective mixing of the Al–15Sn–5Pb powder system, reducing the impact of gravitational segregation and improving the uniformity of soft-phase (Sn + Pb) particle distribution. This allows for its further application in selective laser melting (SLM) technology.

2. The discrete element method with the modified Hertz–Mindlin model demonstrated high reliability in predicting the homogeneity evolution of powder mixtures, which was confirmed by experimental data.

3. It was established that reducing the size of soft-phase (Sn + Pb) agglomerates and minimizing component distribution deviations occur at a mixing time of 60 to 120 min, making this interval recommended for practical applications.

4. The obtained results can be utilized to improve powder preparation quality for additive manufacturing technologies and to develop new powder materials with enhanced performance characteristics.