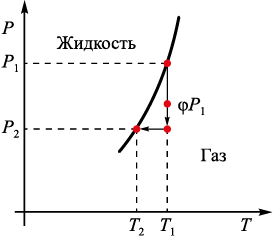Перейти к:
Физико-математическая модель доставки паров кремния в ходе высокотемпературного силицирования пористых углеродных материалов
https://doi.org/10.17073/1997-308X-2024-3-49-61
Аннотация
Разработана новая физико-математическая модель транспорта паров кремния в условиях среднего вакуума, позволяющая объяснить аномально интенсивный массоперенос кремния в ходе высокотемпературного силицирования пористого углеродного материала. Выведена формула, показывающая, как изделие должно быть переохлаждено, чтобы в его порах шел процесс конденсации. Получено модифицированное уравнение диффузии для количественного определения распределения концентрации газообразного кремния в реторте, что крайне востребовано при реализации технологии карбидизации углеродного волокна и последующего полного насыщения пор силицируемого изделия непрореагировавшим кремнием. Введен и количественно оценен новый параметр, показывающий вклад конвективного транспорта в общий массоперенос кремния через среду стороннего газа, роль которого играет аргон. Найдено точное аналитическое решение этого уравнения в одномерной постановке для слоя пористой среды с плоской поверхностью. Решение имеет вид логарифмического профиля и позволяет вычислить поток газообразного кремния на входе в изделие. Иллюстрация работоспособности предлагаемого подхода, более приближенная к действительности, производится путем двумерных расчетов, выполненных методом конечных разностей. В то же время предлагаемая модель легко обобщается на случай трехмерных вычислений со сложной геометрией, с чем всегда приходится иметь дело в реальном технологическом процессе. Расчеты в двумерной постановке выполнены для двух модельных систем, когда зеркало расплава и изделие параллельны или перпендикулярны друг другу. Исследована динамика распространения паров кремния в реторте. Показано, что в рассматриваемых условиях газообразный кремний после начала парообразования заполняет все пространство реторты за характерное время менее 1 с.
Для цитирования:
Агеева М.В., Демин В.А., Демина Т.В. Физико-математическая модель доставки паров кремния в ходе высокотемпературного силицирования пористых углеродных материалов. Известия вузов. Порошковая металлургия и функциональные покрытия. 2024;18(3):49-61. https://doi.org/10.17073/1997-308X-2024-3-49-61
For citation:
Ageeva M.V., Demin V.A., Demina T.V. Physical and mathematical model of the silicon vapor transport during high-temperature silicification of a porous carbon media. Powder Metallurgy аnd Functional Coatings (Izvestiya Vuzov. Poroshkovaya Metallurgiya i Funktsional'nye Pokrytiya). 2024;18(3):49-61. https://doi.org/10.17073/1997-308X-2024-3-49-61
Введение
В настоящее время композиционные материалы (КМ) занимают серьезную нишу во всех отраслях промышленности и используются как для изготовления отдельных изделий, так и в качестве покрытий, обладающих специальными свойствами. Активное применение КМ обусловлено их уникальными свойствами. В частности, КМ, полученные путем высокотемпературного силицирования пористого углеродного каркаса, обладают высокими антиокислительными свойствами, низкой плотностью и, при должной технологии, высокой степенью герметичности [1; 2]. Технологически процесс высокотемпературного силицирования осуществляется в условиях среднего вакуума в атмосфере несущего инертного газа, роль которого играет аргон [3].
Ранее были попытки разработать полную физико-математическую модель технологии парофазного силицирования, которая включала количественное описание процесса заполнения пор внутри образца и, в дополнение, решение сопряженной задачи переноса паров кремния от зеркала расплава к изделию [4–6]. Однако в указанных работах уже на этапе численного моделирования диффузионного транспорта паров кремния в рабочем пространстве реторты возникало непреодолимое противоречие результатов расчетов и экспериментальных данных. Физико-математическая модель, заложенная в основу описания процесса, предполагала, что основным механизмом переноса является диффузия, а на зеркале расплава при заданной рабочей температуре концентрация паров кремния не может превышать значение концентрации насыщенных паров. По результатам решения уравнения диффузии даже при условии полного поглощения кремния на поверхности образца массовый поток пара оказывается недостаточен, чтобы за разумное время полностью силицировать изделие. В работах [4–6] предсказывалось, что для того, чтобы в ходе силицирования пар кремния преодолел диффузионный барьер в виде атмосферы остаточного газа, требуется ставить тигли с расплавом как можно ближе к изделию, в то время как в реальности этот фактор не является определяющим, и зачастую некоторые области крупногабаритного изделия остаются «сухими», несмотря на то, что тигли с расплавом кремния расположены максимально близко к поверхности образца.
Более того, опыт показывает, что насыщение пористых углеродных матриц кремнием возможно, и разнообразные варианты этой методики уже давно серийно реализуются во многих технологических процессах. Таким образом, по-прежнему крайне актуальной является задача количественного определения массопотока паров кремния через поверхность заготовки для осуществления контроля технологического процесса при формировании функциональных покрытий или управления процессом глубокой пропитки пористого материала.
Все известные на сегодняшний день современные технологии производства высокотемпературных КМ непрерывно совершенствуются [7–9] и вследствие усложнения требуют на разных этапах реализации использования более современных подходов, включая построение новых физико-математических моделей для описания происходящих процессов. Применительно к реальным условиям производства процесс доставки газообразного кремния от зеркала расплава до поверхности изделия в ходе высокотемпературного силицирования углеродного пористого материала должен описываться сложной системой дифференциальных уравнений в частных производных, и для его адекватного моделирования необходим учет множества осложняющих факторов, включая конвективный массоперенос [10]. В то же время технология является существенно трехмерной и требует сильной детализации расчетной сетки по причине наличия в реторте множества тиглей с расплавом и их сложного расположения в рабочем пространстве печи [7]. В настоящий момент осуществить полноценное 3D-численное моделирование этого процесса не представляется возможным. В результате имеющиеся модели для описания переноса газообразного кремния в рабочем пространстве промышленной установки в ходе высокотемпературного силицирования ограничиваются простейшими подходами. Вследствие того, что данный процесс осуществляется в условиях среднего вакуума и при чрезвычайно высоких температурах выше точки плавления кремния (T > 1683 К), считалось, что диффузия играет решающую роль в обеспечении транспорта газообразного кремния от расплава к изделию, и только она учитывалась в физико-математических моделях [4–6].
Использование реальных значений коэффициента диффузии в уравнении переноса не позволяет обеспечить наблюдаемый в опыте подвод того количества кремния, который необходим для полноценного силицирования изделия. В результате налицо имеет место парадоксальная ситуация, так как факты говорят сами за себя: в экспериментах изделие при определенных условиях все же может быть насыщено требуемым количеством кремния, а существующая теория утверждает, что это невозможно. Это означает, что все физические условия, необходимые для успешной реализации процесса силицирования, до сих пор остаются не до конца ясными.
Таким образом, цель настоящей работы заключается в том, чтобы объяснить наблюдающийся экспериментально аномально сильный перенос газообразного кремния от зеркала расплава к поверхности изделия. Задачей теоретического исследования является построение более совершенной физико-математической модели переноса паров кремния в рабочем пространстве реторты. Необходимо опробовать эту модель на примере конкретных постановок и показать ее бо́льшую состоятельность по сравнению с чисто диффузионным аналогом.
Анализ базовых уравнений
Уравнение классической диффузии в трехмерной постановке [11], которое стандартно используется для расчета распределения паров кремния в реторте, имеет вид
\[\frac{{\partial C}}{{\partial t}} = D\left( {\frac{{{\partial ^2}C}}{{\partial {x^2}}} + \frac{{{\partial ^2}C}}{{\partial {y^2}}} + \frac{{{\partial ^2}C}}{{\partial {z^2}}}} \right)\,,\]
где D – коэффициент диффузии (полагается константой), C – массовая концентрация. Это известное дифференциальное уравнение в частных производных второго порядка параболического типа. В стационарном случае (∂/∂t = 0) задача упрощается и сводится к уравнению Лапласа ΔC = 0.
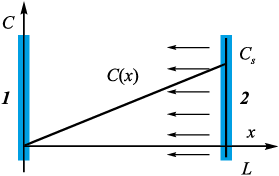
Для начала, не вдаваясь в тонкости промышленной технологии, имеет смысл, следуя работе [10], рассматривать процесс в виде простейшей модельной постановки, когда поверхности изделия и расплава представляют собой две параллельные плоскости, находящиеся на расстоянии L друг от друга (рис. 1). Действием силы тяжести в дальнейшем будем пренебрегать. Пусть на зеркале расплава задается концентрация насыщенных паров кремния C(L) = Cs , а на левой границе, ввиду полного поглощения газообразного кремния пористой средой, поддерживается условие C(0) = 0.
Рис. 1. Геометрия задачи |
В одномерной постановке уравнение Лапласа с этими граничными условиями приводит к единственному нетривиальному решению в виде линейной зависимости
\[C(x) = \frac{{{C_s}}}{L}x\,,\]
которое схематично представлено на рис. 1. Характерное расстояние L между зеркалом расплава и изделием составляет порядка 0,5÷1,5 м.
Согласно экспериментальным данным, давление насыщенного пара для кремния при температурах, не сильно превышающих точку плавления кремния, весьма мало и равно по порядку величины ps = 10 Па [12; 13]. Объемная концентрация для газообразного кремния в состоянии насыщения вычисляется через давление насыщенных паров с помощью уравнения состояния идеального газа и при рабочей температуре T = 1800 К дает значение порядка ns ~ 4·1020 м\(^–\)3. Сравним предсказываемую теоретически плотность потока кремния со значением, наблюдаемым в эксперименте. Если перенос кремния определяется только диффузией, то в этом случае плотность потока кремния определяется законом Фика:
| \[{\bar j_{\rm{к}}} = - \rho D\nabla C = - D\nabla {\rho _{\rm{к}}}\,,\] | (1) |
где ρ – плотность газа, С – массовая концентрация. Коэффициент диффузии атомов кремния для условий среднего вакуума в атмосфере аргона оценим с помощью известной формулы молекулярно-кинетической теории [14]:
| \[D = \frac{3}{8}\frac{{kT}}{{{\sigma _{12}}p}}\sqrt {\frac{{\pi kT}}{{2{\mu _{12}}}}} = \frac{3}{8}\frac{{{{\left( {kT} \right)}^{3/2}}}}{{d_{{\rm{Si}}}^{\rm{2}}p\sqrt {\pi {m_0}} }}.\] | (2) |
Здесь σ12 – эффективное сечение рассеяния для двух частиц, μ12 – приведенная масса, k – постоянная Больцмана. Для двух примерно одинаковых по массе и размерам частиц имеем σ12 = πd2, μ12 = m0 /2. Масса одного атома кремния равна m0 = 4,7·10\(^–\)26 кг. Из табличных данных возьмем диаметр атома кремния dSi = 2,3·10\(^–\)10 м. В результате получаем D = 0,7 м2/с. Столь непривычно большое значение коэффициента диффузии связано с двумя факторами: сильной разреженностью среды в условиях среднего вакуума и высокой температурой.
Принимая во внимание, что плотность кремния на зеркале расплава составляет ρк = pк μк /(RT) = 1,87·10\(^–\)5 кг/м3, формула (1) предсказывает весьма малое значение плотности потока кремния: jк = 2,62·10\(^–\)5 кг/(м2·с). По оценкам технологов, занимающихся силицированием углеродных изделий, этого явно недостаточно, чтобы при имеющейся пористости материала за разумное время произвести полную закупорку пор. Однако в действительности при выполнении некоторых условий, выявленных технологами экспериментально, различные по форме изделия все же успешно насыщаются кремнием. Таким образом, можно считать надежно установленным положение, согласно которому все неудачи в ходе технологического процесса определяются совсем другими факторами, а именно распределением температуры на изделии [15]. Очевидно, что переход паров кремния из газообразного состояния в жидкое или твердое возможен только в случае, если изделие имеет более низкую температуру, нежели пар [16–18]. После выравнивания температур процесс силицирования за счет конденсации в пористом материале по идее должен прекратиться. В этом случае окружающий газ и изделие приходят в термодинамическое равновесие. Для общего понимания вычислим, на сколько необходимо переохладить изделие, чтобы на нем шел процесс конденсации кремния. Граница между двумя фазами (паром и жидкостью) определяется так называемым уравнением Клапейрона–Клаузиуса [19], которое, как известно, выводится из условия непрерывности термодинамического потенциала:
| \[\frac{{dP}}{{dT}} = \frac{q}{{T\left( {{v_1} - {v_2}} \right)}},{\rm{ }}{v_1} = \frac{{{V_1}}}{{{m_1}}},{\rm{ }}{v_2} = \frac{{{V_2}}}{{{m_2}}}.\] | (3) |
Здесь q – удельная теплота фазового перехода; P – давление газа; T – температура; v1 , v2 – удельные объемы, занимаемые соответственно паром и жидкостью, м3/кг. Заметим, что для пара и жидкости справедливо условие v1 \( \gg \) v2 , в результате уравнение (3) может быть упрощено до вида
| \[\frac{{dT}}{{dP}} = \frac{{vT}}{q}.\] | (4) |
В рассматриваемом приближении индекс, соответствующий удельному объему пара, не нужен, и в дальнейших расчетах он опускается. Кривая фазового перехода схематично представлена на рис. 2.
Рис. 2. Фазовые состояния на диаграмме P–T |
Будем считать, что реальные условия для паров кремния в ходе силицирования недалеки от состояния насыщения и отвечают температуре T1 . Очевидно, что для перехода в пересыщенное состояние при том же давлении необходимо понизить температуру изделия. Пусть предполагаемое давление насыщенного пара при температуре T1 равно P1 . Так как в действительности пар не является насыщенным, его реальное давление равно φP1, где φ – относительная влажность пара. В реальных условиях при понижении температуры давление пара автоматически тоже уменьшается до значения P2 .
Объем и масса газа остаются прежними, поэтому имеем по факту изохорный процесс, который описывается уравнением
\[\frac{{{P_2}}}{{{T_2}}} = \frac{{\varphi {P_1}}}{{{T_1}}}.\]
Изохорный процесс изображен на рис. 2 стрелками, при этом конечное состояние характеризуется пороговыми давлением и температурой, соответствующими точке конденсации. Отсюда выражаем давление в конечном состоянии: P2 = φP1 T2 /T1 .
С другой стороны, в каждой точке на фазовой диаграмме состояние газа описывается уравнением Менделеева–Клапейрона, из которого можно выразить удельный объем через давление и температуру пара:
| \[\frac{{PV}}{T} = \frac{{Rm}}{\mu },{\rm{ }}\frac{{Pv}}{T} = \frac{R}{\mu },{\rm{ }}v = \frac{{RT}}{{\mu P}}.\] | (5) |
где V – общий объем, μ – молярная масса, R – универсальная газовая постоянная, v – объем, приходящийся на единицу массы. Для простоты рассуждений заменим производную в уравнении Клапейрона–Клаузиуса (4) конечными разностями, исключив попутно удельный объем с помощью уравнения (5):
| \[\frac{{{T_2} - {T_1}}}{{{P_2} - {P_1}}} = \frac{{v{T_1}}}{q},{\rm{ }}\frac{{{T_2} - {T_1}}}{{{P_2} - {P_1}}} = \frac{{RT_1^2}}{{q\mu {P_1}}}.\] | (6) |
Заметим, что производная в уравнении (6) с математической точки зрения представляет собой так называемую одностороннюю разность в точке 1. Далее подставим выражение для давления P2 при изопроцессе в уравнение (6) и найдем оттуда искомую разность температур. Начальное давление P1 в окончательном выражении сокращается, и, на первый взгляд, кажется странным, что от него ничего не зависит. Однако однозначная полная информация о начальном состоянии пара кремния все же содержится в этом уравнении, так как помимо температуры в нем присутствует относительная влажность пара. Простые арифметические действия позволяют выразить окончательную разность температур:
| \[{T_2} - {T_1} = \frac{{RT_1^2\left( {\varphi - 1} \right)}}{{\mu q - R{T_1}\varphi }}.\] | (7) |
Из формулы (7) видно, что разность температур отрицательна, что указывает на необходимость понижения температуры изделия по сравнению с температурой газа. В качестве примера оценим разность температур для реалистичных значений параметров: φ = 0,8, q = 13,8·106 Дж/кг, μ = 28·10\(^–\)3 кг/моль, T1 = 1790 К. Выбранное значение температуры T1 превышает точку плавления кремния на 102 К. Это не выходит за рамки рабочего диапазона температур в реторте. В результате имеем T2 – T1 = –15 К.
Иными словами, расчет показывает, что необходимая разность температур невелика, но, как вытекает из анализа теплофизической обстановки в условиях реального производства, становится ясно, что этот температурный фактор абсолютно не контролируется и данное требование, скорее всего, не выполняется в ходе натурного технологического процесса. Как показывают оценки, особенно негативным в этом плане является наличие так называемой «тепловой шапки» в верхней области рабочего пространства внутри реторты. Это объясняет, почему при силицировании крупногабаритных изделий их верхняя часть зачастую пропитывается кремнием хуже, чем нижняя. Причина в том, что у основания изделия температура бо́льшую часть времени значительно ниже, чем в верхней области. Все физические факторы, отвечающие за создание неоднородности в распределении температуры вдоль вертикали в реторте, работают только на усиление указанной стратификации. Конвективный фактор, расположение вакуумных насосов вблизи дна, низкая теплоизоляция у основания рабочего пространства, боковые нагреватели, расположенные достаточно высоко от основания, – все это приводит к возникновению специфической тепловой стратификации с градиентом температуры, направленным преимущественно вертикально вверх. Поэтому требуемая формулой (7) разность температур между парами кремния и изделием, если и может возникнуть, то только вблизи нижней границы рабочего пространства.
Таким образом, вернемся к действительно актуальному вопросу подведения паров кремния к изделию, так как понятно, что его необходимо решать независимо от проблемы организации нагрева в реторте в ходе силицирования.
Новая физико-математическая модель
переноса паров кремния
Будем предполагать, что в рассматриваемых условиях помимо диффузионного присутствует дополнительный конвективный механизм переноса. Более общее уравнение транспорта примеси как сплошной среды с учетом этого фактора [11] записывается в виде
| \[\frac{{\partial C}}{{\partial t}} + \left( {\vec V\nabla } \right)C = D\Delta C,\] | (8) |
где \(\vec V\) – макроскопическая (массовая) скорость физически малого элемента газа.
Главной проблемой при использовании уравнения (8) является вопрос о его замыкании. В рамках механики сплошных сред динамика флюида в общем случае определяется уравнением Навье–Стокса [11]. В трехмерном случае это три нелинейных дифференциальных уравнения в частных производных для трех компонент скорости vi (x, y, z, t), где i = 1, 3. В эти уравнения входят еще две неизвестные величины – давление и переменная плотность, которые тоже подлежат определению в ходе решения задачи. В результате к системе уравнений добавляются еще два: закон сохранения массы в дифференциальной форме и уравнение состояния. Таким образом, итоговая система уравнений становится чрезвычайно громоздкой и трудноразрешимой.
В настоящее время прямое численное моделирование рассматриваемых процессов в полной трехмерной постановке весьма затруднительно даже с помощью высокопроизводительных суперкомпьютеров. Проблема заключается в том, чтобы попытаться сформулировать задачу в упрощенной постановке так, чтобы, с одной стороны, учесть все физические факторы, важные для адекватного описания указанных процессов, а с другой стороны, избежать использования излишне сложных моделей, чтобы задача считалась за разумное время и не требовала бы излишних вычислительных мощностей.
Следуя подходу, реализованному в [10], рассмотрим в полной постановке уравнение Навье–Стокса и оценим вклад каждого слагаемого, подразумевая, что газообразный кремний перемещается через материнский флюид аргона, как через пористую среду. В гидродинамике пористых сред [20] необходимо отличать поровую скорость \(\vec v\) и скорость фильтрации \({\bf{\vec \upsilon }}\). Скорость фильтрации определяется через общий расход флюида и связана с поровой скоростью соотношением \({\bf{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over \upsilon } }} = \phi \vec v.\) Здесь ϕ – пористость материала. Для поровой скорости в среде имеем исходное уравнение движения [20]:
\[{\rho _f}\left( {\frac{{\partial \vec v}}{{\partial t}} + \left( {\vec v\nabla } \right)\vec v} \right) = - \nabla p - \frac{\eta }{\kappa }{\bf{\vec \upsilon }}.\]
Здесь ρf – плотность движущейся через пористую среду жидкости, η – динамическая вязкость, κ – проницаемость, p – поле давления. В этом уравнении предполагается, что трение линейно зависит от скорости фильтрации. Сила тяжести для простоты не учитывается. Переходя полностью к скорости фильтрации, получаем
| \[{\rho _f}\left( {{\phi ^{ - 1}}\frac{{\partial {\bf{\vec \upsilon }}}}{{\partial t}} + {\phi ^{ - 2}}\left( {{\bf{\vec \upsilon }}\nabla } \right){\bf{\vec \upsilon }}} \right) = - \nabla p - \frac{\eta }{\kappa }{\bf{\vec \upsilon }}.\] | (9) |
Теперь можно оценить слагаемые в левой и правой частях этого уравнения, содержащие скорость. Наименее тривиальным параметром в данном уравнении является проницаемость κ. В нашем случае это проницаемость газообразного аргона по отношению к потоку атомов кремния. В отношении подвижных атомов несущей среды (аргона) можно говорить лишь о модельном характере этого газа как пористого материала с некоторой эффективной проницаемостью. Будем иметь в виду модель, согласно которой газообразный кремний как некий флюид фильтруется через несущую среду за счет того, что пар кремния в избытке рождается на зеркале расплава и поглощается на противоположной границе. Ввиду крайней разреженности несущей среды ожидается, что проницаемость κ будет иметь аномально большое значение. В то же время пористость близка к единице, так как атомы аргона, как рассеивающие центры, занимают чрезвычайно малый объем.
Пусть среда представляет собой систему из небольших твердых сферических центров, которые омываются гидродинамическим потоком. Межатомное расстояние в аргоне по порядку величины равно длине свободного пробега
\[l = \frac{{kT}}{{\sqrt 2 \pi {d^2}p}} = \frac{{1,38 \cdot {{10}^{ - 23}} \cdot 1800}}{{\sqrt 2 \pi {{\left( {1,4 \cdot {{10}^{ - 10}}} \right)}^2} \cdot 100}} = 5,6 \cdot {10^{ - 3}}{\rm{ м}}.\]
Здесь для диаметра атома аргона взято значение d = 1,4·10\(^–\)10 м. Согласно технологическому процессу, парциальное давление аргона составляет по порядку величины 100 Па. В итоге имеем для проницаемости κ ~ l2 = 3,1·10\(^–\)5 м2.
Однако эта оценка дает несколько заниженное значение проницаемости, так как справедлива в случае плотной упаковки препятствий. Для более точной ее оценки воспользуемся известной формулой Козени–Кармана [20]. Эта формула имеет в теории пористых сред широкое применение и выводится из самых общих геометрических соображений. В результате получаем
\[\kappa = \frac{{{\phi ^3}{d^2}}}{{{{\left( {1 - \phi } \right)}^2}}} = 5 \cdot {10^{ - 4}}{\rm{ м}}{{\rm{}}^{\rm{2}}}.\]
Здесь ϕ – пористость несущей среды (аргона), d – характерный размер обтекаемого препятствия (в нашем случае это атомы аргона).
Еще один важный параметр – это макроскопическая скорость элемента газа (скорость фильтрации). Будем считать, что при испарении атомы кремния отрываются от поверхности расплава со среднеквадратичной скоростью, значение которой при T = 1800 К составляет ~1250 м/с. Осредняя по всевозможным направлениям, получаем величину проекции скорости на нормаль (скорость фильтрации) v ~ 310 м/с. Оценим теперь величину каждого слагаемого в уравнении (9), принимая во внимание, что пористость такой среды близка к единице и рассматривается стационарное движение (∂/∂t = 0):
\[\begin{array}{c}\left| {{\rho _f}{\phi ^{ - 2}}\left( {{\bf{\vec \upsilon }}\nabla } \right){\bf{\vec \upsilon }}} \right| \sim {\rho _f}\frac{{{{\bf{\upsilon }}^2}}}{L} = 2 \cdot {10^{ - 5}}\frac{{{{310}^2}}}{{0,5}} = 3,8,\\\left| {{\rho _f}{\phi ^{ - 1}}\frac{{\partial {\bf{\vec \upsilon }}}}{{\partial t}}} \right| = 0,{\rm{ }}\left| {\frac{{\eta {\bf{\vec \upsilon }}}}{\kappa }} \right| = \frac{{3,5 \cdot {{10}^{ - 4}} \cdot 310}}{{5 \cdot {{10}^{ - 4}}}} = 217.\end{array}\]
Из этих оценок видно, что вязкое слагаемое является доминирующим в этом уравнении. А именно: как инерционное слагаемое, так и слагаемое, отвечающее за нестационарность процессов, пренебрежимо малы по сравнению с вязким членом:
\[\left| {\frac{{\eta {\bf{\vec \upsilon }}}}{\kappa }} \right| \gg \left| {{\rho _f}{\phi ^{ - 2}}\left( {{\bf{\vec \upsilon }}\nabla } \right){\bf{\vec \upsilon }}} \right|.\]
В результате из уравнения (9) имеем выражение для скорости в виде известного закона Дарси [20]:
| \[{\bf{\vec \upsilon }} = - \frac{\kappa }{\eta }\nabla {p_{\rm{к}}}.\] | (10) |
За счет испарения на зеркале расплава и поглощения на изделии имеем средний градиент плотности паров кремния. Так как давление газа в общем случае пропорционально плотности, это порождает градиент давления кремния, который может выступать в роли дополнительной движущей силы помимо диффузии. Парциальное давление кремния, согласно уравнению состояния идеального газа, равно pк = nкkT, где nк = Nк /V – число атомов кремния в единице объема. Выразим nк через массовую концентрацию C. По определению под массовой концентрацией будем понимать
\[C = \frac{{{m_{\rm{к}}}}}{{{m_{\rm{а}}} + {m_{\rm{к}}}}} = \frac{{{\rho _{\rm{к}}}}}{{{\rho _{\rm{а}}} + {\rho _{\rm{к}}}}},\]
тогда плотность кремния выражается через относительную массовую концентрацию следующим образом:
| \[{{\rm{\rho }}_{\rm{к}}} = \frac{C}{{1 - C}}{{\rm{\rho }}_{\rm{а}}}.\] | (11) |
Запишем уравнение для парциального давления кремния через плотность кремния и подставим туда соотношение (11):
| \[{p_{\rm{к}}} = \frac{{RT}}{{{\mu _{\rm{к}}}}}\frac{C}{{1 - C}}{{\rm{\rho }}_{\rm{а}}}.\] | (12) |
Далее подставим этот результат в закон Дарси (10), пренебрегая пространственными неоднородностями плотности аргона и температуры в реторте. Также учтем тот факт, что концентрация кремния в действительности никогда не достигает единицы. Аргон или остаточный воздух присутствуют в реторте всегда, и их концентрация примерно на порядок превышает концентрацию паров кремния. В результате разложим множитель C/(1 – C) в ряд по малым C и ограничимся в итоговом выражении первым неисчезающим членом. Закон Дарси (10) приобретает вид
| \[{\bf{\vec \upsilon }} = - \frac{\kappa }{\eta }\nabla {p_{\rm{а}}} = - \frac{\kappa }{\eta }\frac{{RT{\rho _{\rm{к}}}}}{{{\mu _{\rm{к}}}}}\nabla C.\] | (13) |
Тем не менее в уравнение (8) по смыслу входит среднемассовая скорость
\[\vec V = \frac{{{\rho _{\rm{a}}}{{{\bf{\vec \upsilon }}}_{\rm{a}}} + {\rho _{\rm{к}}}{{{\bf{\vec \upsilon }}}_{\rm{к}}}}}{{{\rho _{\rm{a}}} + {\rho _{\rm{к}}}}} = \frac{{{\rho _{\rm{к}}}{{{\bf{\vec \upsilon }}}_{\rm{к}}}}}{{{\rho _{\rm{a}}} + {\rho _{\rm{к}}}}} \approx \frac{{{\rho _{\rm{к}}}{{{\bf{\vec \upsilon }}}_{\rm{к}}}}}{{{\rho _{\rm{a}}}}}.\]
Подставляя (13) в эту формулу, исключаем из обобщенного уравнения переноса примеси (8) скорость и получаем окончательно уравнение
| \[\frac{{\partial C}}{{\partial t}} - \frac{{\kappa RT{\rho _{\rm{к}}}}}{{\eta {\mu _{\rm{к}}}}}{\left( {\nabla C} \right)^2} = D\Delta C.\] | (14) |
Теперь это более сложное дифференциальное уравнение в частных производных с нелинейностью типа квадрата градиента концентрации, но для одной переменной C(x, y, z, t). Отметим, что подобные уравнения диффузии с нелинейностями, которые квадратичны градиенту концентрации, встречаются в различных областях физики, однако выводятся иначе. Так, в работах [21; 22] показано, что нелинейное слагаемое данного вида довольно сильно меняет транспортные диффузионные свойства материала, в роли которого выступает ниобат лития, и позволяет объяснить некоторые наблюдаемые эффекты, связанные с насыщением водородом рассматриваемой среды. В общем случае уравнение (14) позволяет решать нестационарные задачи о распределении концентрации в трехмерной постановке.
Аналитическое решение
В первую очередь имеет смысл проанализировать уравнение (14) на предмет наличия стационарного решения. При условии ∂/∂t = 0 уравнение (14) приводится к виду
| \[ - \left( {\nabla C} \right) = \psi \Delta C,{\rm{ }}\psi = \frac{{\eta {\mu _{\rm{к}}}D}}{{\kappa RT{\rho _{\rm{к}}}}},\] | (15) |
где ψ – новый безразмерный параметр. Оценим значение введенного параметра, который определяет условно отношение «диффузионного» механизма переноса к «конвективному». Возьмем величину динамической вязкости из работы [10]. В ней данный параметр оценивался применительно к рассматриваемому процессу силицирования, исходя из известных формул молекулярно-кинетической теории [14]:
\[\frac{{\eta = \frac{1}{3}{{\left( {\frac{2}{\pi }} \right)}^{3/2}}{{\left( {{m_0}kT} \right)}^{1/2}}}}{{d_{{\rm{Ar}}}^2}} = 3.5 \cdot {10^{ - 4}}{\rm{ }}{{\rm{м}}^{\rm{2}}}{\rm{/с}}{\rm{.}}\]
Оценка параметра ψ для значения проницаемости κ = 5·10\(^–\)4 м2 дает ψ = 0,048. Это означает, что в рассматриваемых условиях конвективный перенос вносит существенный вклад в транспорт паров кремния.
В одномерной постановке применительно к геометрии задачи, представленной на рис. 1, уравнение (15) имеет точное решение. А именно, сформулируем краевую задачу для неизвестной функции C(x) в виде обыкновенного дифференциального уравнения второго порядка и двух граничных условий:
\[ - \left( {\frac{{dC}}{{dx}}} \right) = \psi \frac{{{d^2}C}}{{d{x^2}}};{\rm{ }}C(0) = 0,{\rm{ }}C(L) = {C_s}{\rm{.}}\]
Заменой переменной порядок уравнения понижается, и затем оно элементарно интегрируется [23]. В результате, с учетом упомянутых выше однородных граничных условий, получаем логарифмическую зависимость
| \[C(x) = \psi \ln \left\{ {\frac{x}{L}\left[ {\exp \left( {\frac{{{C_s}}}{\psi }} \right) - 1} \right] + 1} \right\}.\] | (16) |
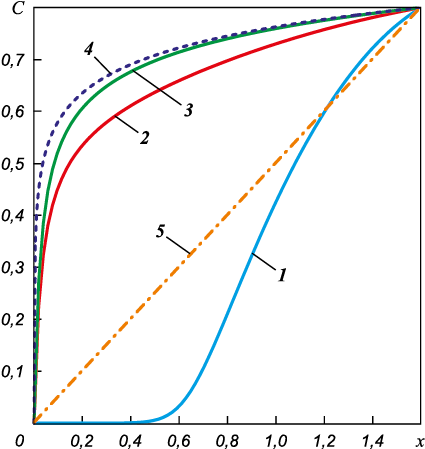
Для полноты можно вычислить производную от этого решения на левой границе. Это значение производной дает плотность потока паров кремния на порядок выше, чем в случае чисто диффузионного переноса: jк = 3,0·10\(^–\)4 кг/(м2·с). Представим в качестве примера график зависимости C(x) для L = 1,6 м. Сейчас решение представляет собой выпуклую функцию. Как видно из рис. 3 (кр. 4), наибольшая производная имеет место как раз на левой границе области определения, т.е. на поверхности изделия. Плотность потока пропорциональна величине производной. Таким образом, учет независимого конвективного переноса паров кремния в дополнение к диффузионному транспорту позволяет объяснить наблюдаемую в экспериментах большую скорость высокотемпературного насыщения углеродного материала в условиях среднего вакуума. В дополнение, пары кремния заполняют теперь практически все рабочее пространство реторты. Только вблизи самого изделия в тонком пограничном слое, ввиду предполагаемого полного поглощения, концентрация паров кремния стремится к нулю. Это хорошо согласуется с данными натурного эксперимента в том смысле, что конденсация кремния может интенсивно проходить в местах реторты, значительно удаленных от тиглей.
Рис. 3. Эволюция профиля концентрации в разные моменты времени |
Одномерное нестационарное решение
Проведем теперь расчет нестационарной задачи. В первую очередь будем интересоваться одномерным решением.
Уравнение (14) является нелинейным, поэтому получить его нестационарное решение проще всего численно, методом конечных разностей [24]. Схемы дискретизации первого порядка точности использовались для аппроксимации производных как по времени, так и по пространству. Первый порядок точности для пространственных производных с «разностями назад» применялся для обеспечения устойчивости разностной схемы. Программный код был реализован на языке программирования FORTRAN-90. Число узлов по пространственной координате принималось равным N = 85.
Как видно из динамики концентрационного фронта, представленного для разных моментов времени на рис. 3, решение довольно быстро выходит на установившийся стационарный профиль в виде уже описанной ранее выпуклой функции (графики получены для L = 1,6 м). Результаты расчетов показывают, что время выхода на стационар составляет ~2 с. Сначала пар кремния присутствует только у зеркала расплава (кр. 1 на рис. 3). Затем очень быстро кремний заполняет все пространство внутри реторты (рис. 3, кр. 2, 3). На момент установления (рис. 3, кр. 4) наибольшая производная имеет место на левой границе расчетной области, т.е. на поверхности изделия. Полученное в ходе данного исследования численное решение обобщенного уравнения диффузии паров кремния при силицировании пористого углеродного материала показывает, что газообразный кремний быстро занимает практически весь объем рабочего пространства печи. Иными словами, нет необходимости максимально близко приближать тигли с расплавом кремния к поверхности изделия, как это предполагалось долгое время по результатам предшествующих теоретических работ [4–6].
Расчеты в двумерной постановке
Следующий по сложности этап – это проведение численного моделирования в двумерной постановке. Эти расчеты также были выполнены методом конечных разностей. Была реализована классическая явная схема [24]. В ходе вычислений использовалась равномерная по пространству прямоугольная сетка с разбиением 85:41 (85 узлов вдоль координаты x между зеркалом расплава и образцом, 41 узел по координате y – вдоль поверхности изделия). В 2 раза большее число узлов вдоль оси x объясняется необходимостью разрешения пограничного слоя вблизи изделия на конечном этапе установления. Высота образца равна H = 0,4 м, расстояние от расплава до изделия – L = 0,6 м. На верхней и нижней гранях ставилось условие непроницаемости. Как и в одномерном случае, для аппроксимации производных по времени и по пространству использовались схемы дискретизации первого порядка точности. Для обеспечения устойчивости разностной схемы производные по «потоку» имели первый порядок точности и вычислялись как «разности назад». Теперь процесс переноса паров кремния описывается следующим нестационарным уравнением:
| \[\frac{{\partial C}}{{\partial t}} - {D_c}\left[ {{{\left( {\frac{{\partial C}}{{\partial x}}} \right)}^2} + {{\left( {\frac{{\partial C}}{{\partial y}}} \right)}^2}} \right] = D\left( {\frac{{{\partial ^2}C}}{{\partial {x^2}}} + \frac{{{\partial ^2}C}}{{\partial {y^2}}}} \right).\] | (17) |
В это уравнение входят два размерных управляющих параметра. Один из них по смыслу – параметр конвективного транспорта:
| \[{D_c} = \frac{{\kappa RT{\rho _{\rm{к}}}}}{{\eta {\mu _{\rm{к}}}}},\] | (18) |
второй – коэффициент диффузии D; оба имеют одинаковую размерность [м2/с]. Первый параметр описывает конвективный механизм переноса, второй – чисто диффузионный. Теперь (17) – это двумерное нестационарное дифференциальное уравнение в частных производных с той же нелинейностью типа квадрата градиента концентрации. Расчеты были выполнены для L = 0,6 м (длина массива), H = 0,4 м (высота образца), Dc = 57,1 м2/с (конвективный параметр), D = 0,7 м2/с (коэффициент диффузии). В начальный момент времени пары кремния отсутствуют в пространстве внутри реторты. На правой границе задается постоянное значение концентрации, соответствующее насыщению, на левой – условие полного поглощения.
Результаты и их обсуждение
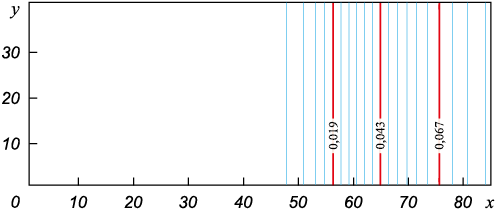
Как видно из динамики концентрационного фронта, представленного для разных моментов времени на рис. 4 и 5, решение по-прежнему довольно быстро выходит на установившийся стационарный профиль в виде выпуклой поверхности, как и в одномерном случае. На начальном этапе, который длится всего тысячные доли секунды, пары кремния присутствуют только справа вблизи зеркала расплава (рис. 4). Далее наблюдаются заполнение парами пространства реторты и укручение концентрационного профиля. Отметим, что концентрационный фронт по мере продвижения к поверхности изделия все время остается плоским.
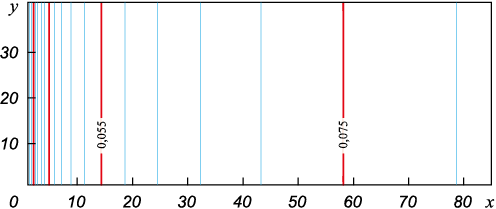
Рис. 4. Изолинии концентрации паров кремния на начальном этапе при t = 0,004 c
Рис. 5. Поле изолиний концентрации кремния на момент установления при t = 1,0 с |
Расчеты показывают, что время выхода на стационар составляет порядка 0,5 с. Наибольшая производная на финальной стадии установления (рис. 5) по-прежнему имеет место на левой границе расчетной области, т.е. на поверхности изделия. Отметим, что плотность потока пропорциональна величине производной в этой точке. Таким образом, учет независимого конвективного переноса паров кремния в дополнение к диффузионному транспорту подтверждает наблюдаемую в экспериментах достаточно большую скорость высокотемпературного насыщения углеродного материала в условиях среднего вакуума, в отличие от значения потока кремния, предсказываемого классическим уравнением диффузии.
Таким образом, необходимо еще раз подчеркнуть, что единственной причиной, по которой крупногабаритное изделие в эксперименте оказывается недостаточно насыщенным кремнием, является неудачный теплофизический режим всего процесса, ход которого определяется конструкционными особенностями печи.
Эти негативные факторы обсуждались ранее в работе [15], в которой была продемонстрирована возможность полного силицирования изделия за разумное время. Иными словами, для прохождения первичной химической реакции карбидизации углеродного волокна и дальнейшей конденсации паров кремния в порах материала требуется технология с более строгим контролем температуры на поверхности изделия, а не манипуляции с перестановкой тиглей. Если поверхность образца параллельна зеркалу расплава, как это предполагалось в первоначальной постановке, то линии тока макроскопического движения кремния представляют собой прямые траектории, перпендикулярные этим поверхностям. При этом волновой фронт паров кремния устойчив, является в каждый момент времени плоским и перемещается от расплава к изделию так, что можно даже использовать условие однородности по координате у. Однако на практике в поле тяжести поверхность зеркала расплава всегда горизонтальна, так как расплав кремния находится в тиглях. В то же время изделие ставится в реторте вертикально на некотором расстоянии от тиглей, которых может быть несколько. В результате важно понять, изменится ли характер распространения паров кремния в реторте при более сложных взаимных расположениях источника паров кремния и поглощающей поверхности.
Проанализируем теперь более реалистичную конфигурацию в виде прямоугольной реторты, изображенной на рис. 6, с поглощающей кремний левой вертикальной границей 1 и горизонтальным зеркалом расплава 2, находящимся на расстоянии 2L/3 от образца. Сама поверхность расплава имеет размер L/3. На всех остальных участках реторты ставится условие непроницаемости.
Рис. 6. Конфигурация с горизонтальным линейным источником паров кремния |
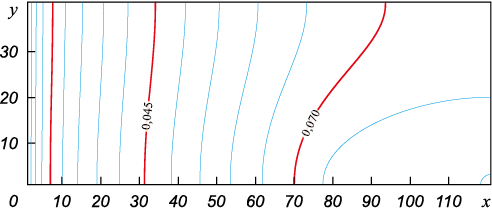
Расчет проводился на сетке 121:41. Высота образца составляла H = 0,4 м, длина расчетной области – L = 1,2 м. При данной пропорции размер зеркала расплава составляет Δ = 0,4 м. Результаты численного моделирования системы в такой конфигурации представлены на рис. 7, 8 для двух моментов времени: на этапе установления (при t = 0,005 c) и в конечном состоянии, близком к стационарному (t = 0,1 c). Видно, что стационарное распределение устанавливается в системе фактически так же быстро, как и для предыдущей конфигурации (за время порядка 1 с). Также расчеты показывают, что кремний по-прежнему занимает практически все рабочее пространство внутри реторты за исключением относительно тонкого пограничного слоя вблизи поглощающего участка поверхности. Из рис. 7, 8 видно, что пары кремния практически с одинаковой интенсивностью распространяются во все стороны от зеркала расплава. Атомы кремния достигают поверхности изделия практически за то же время, что и в предыдущем случае, когда поверхности были параллельны друг другу.
Рис. 7. Поле концентрации кремния на начальном этапе
Рис. 8. Поле концентрации кремния на момент установления |
Результаты расчетов показывают, что разреженный газ (аргон), через который происходит проникновение паров кремния от зеркала расплава к образцу, сам по себе не является главным сдерживающим фактором, ограничивающим массоперенос кремния. По крайней мере, разные конфигурации взаимного расположения источника паров кремния и поглощающей поверхности не сильно меняют время выхода на стационарное состояние.
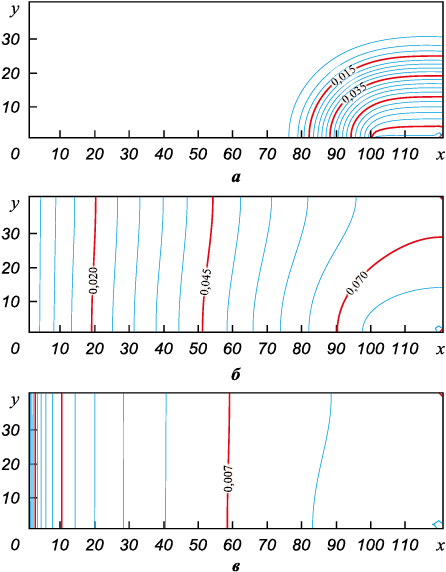
Покажем, что гораздо более серьезным управляющим параметром в задаче является соотношение площадей испаряющей и поглощающей поверхностей. Уменьшим теперь линейный размер поверхности, на которой имеет место испарение, до Δ = 0,2 м, оставив неизменными высоту изделия H = 0,4 м и длину реторты L = 1,2 м. Все остальные параметры оставим прежними. Изолинии и двумерные поверхности поля концентрации для этой ситуации представлены на рис. 9, а, б.
Рис. 9. Поле концентрации кремния |
На рис. 9, а изображен начальный момент времени, пока пары еще не распространились на весь объем. Однако, как видно из рис. 9, б, при меньших размерах зеркала расплава (разница по сравнению с предыдущим случаем составляет 2 раза) в момент времени t = 0,1 с стационарное состояние еще не достигается.
Расчеты показывают, что для установления стационарного режима для концентрационного профиля теперь требуется примерно в 2 раза больше времени, нежели в предыдущем случае. Поле концентрации для зеркала расплава при t = 1,0 c представлено на рис. 9, в. Далее поле концентрации практически перестает меняться с течением времени. Этот результат физически понятен, так как заполнение пространства внутри реторты парами кремния требует определенного времени, и оно напрямую связано с количеством кремния, испаряющегося за единицу времени с поверхности источника. При уменьшении длины зеркала расплава это время закономерно пропорционально увеличивается.
Заключение
Полученные в ходе данного исследования аналитическое и численное решения обобщенного уравнения диффузии паров кремния при силицировании пористого углеродного материала показывают, что газообразный кремний быстро занимает практически весь объем рабочего пространства печи. Иными словами, нет необходимости максимально близко приближать тигли с расплавом кремния к поверхности изделия, как это предполагалось долгое время по результатам предшествующих теоретических работ.
Полученные результаты в двумерной постановке подтверждают аналогичные данные, полученные в одномерном случае. Они показывают, что сопротивление сторонних газов диффузионному потоку кремния, конечно, должно присутствовать в реальном технологическом процессе, но классическая диффузия является не единственным механизмом переноса. Обобщение модели с учетом дополнительного конвективного переноса позволяет решить парадокс, согласно которому в эксперименте наблюдается аномально интенсивное насыщение пористого углеродного материала парами кремния, в противовес более ранним теоретическим предсказаниям.
Список литературы
1. Chawla Krishan K. Composite materials. Science and engineering. N.Y.: Springer, 2012. 542 p.
2. Shang J. Durability testing of composite aerospace materials based on a new polymer carbon fiber-reinforced epoxy resin. Fluid Dynamics & Material Processing. 2023;19(9): 2315–2327. https://doi.org/10.32604/fdmp.2023.026742
3. Shikunov S.L., Kurlov V.N. SiC-based composite materials obtained by siliconizing carbon matrices. Journal of Technical Physics. 2017;62(12):1869–1876. https://doi.org/10.1134/S1063784127120222
4. Гаршин А.П., Кулик В.И., Матвеев С.А., Нилов А.С. Современные технологии получения волокнисто-армированных композиционных материалов с керамической огнеупорной матрицей. Новые огнеупоры. 2017;(4):20–35.
5. Кулик В.И., Кулик А.В., Рамм М.С., Демин С.Е. Разработка модели и численное исследование процессов получения композитов с SiC матрицей методом парофазного силицирования. В сб. матер. IV Междунар. конф. «Функциональные наноматериалы и высокочистые вещества» (Суздаль, 1–5 октября 2012 г.). М.: ИМЕТ РАН, 2012. С. 240–242.
6. Кулик В.И., Кулик А.В., Рамм М.С., Демин С.Е. Численное исследование градиентных газофазных процессов получения керамоматричных композитов с SiC матрицей. В сб. матер. V Междунар. конф. «Функциональные наноматериалы и высокочистые вещества» (Суздаль, 6–10 октября 2014 г.). М.: ИМЕТ РАН, 2014. С. 128–129.
7. Щурик А.Г. Искусственные углеродные материалы. Пермь: Изд-во УНИИКМ, 2009. 342 с.
8. Тимофеев А.Н., Разина А.С., Тимофеев П.А., Бодян А.Г. Расчет глубины проникновения реакции при химическом газофазном осаждении нитрида бора в пористых телах. Известия вузов. Порошковая металлургия и функциональные покрытия. 2023;17(3):38–46. https://doi.org/10.17073/1997-308X-2023-3-38-46
9. Погожев Ю.С., Потанин А.Ю., Рупасов С.И., Левашов Е.А., Волкова В.А., Ташев В.П., Тимофеев А.Н. Структура, свойства и окислительная стойкость перспективной керамики на основе HfB2–SiC. Известия вузов. Порошковая металлургия и функциональные покрытия. 2020;(3):41–54. https://doi.org/10.17073/ 1997-308X-2020-3-41-54
10. Демин В.А., Демина Т.В., Марышев Б.С. Физико-математическая модель переноса газообразного кремния в ходе высокотемпературного силицирования углеродных композитных материалов. Вестник Пермского университета. Физика. 2022;(3):48–55. https://doi.org/10.17072/1994-3598-2022-3-48-55
11. Ландау Л.Д., Лифшиц Е.М. Курс теоретической физики. Т. 6. Гидродинамика. М.: Физматлит, 2001. 736 с.
12. Sevast’yanov V.G., Nosatenko P.Ya., Gorskii V.V., Ezhov Yu.S., Sevast’yanov D.V., Simonenko E.P., Kuznetsov N.T. Experimental and theoretical determination of the saturation vapour pressure of silicon in a wide range of temperatures. Russian Journal of Inorganic Chemistry. 2010;13(55):2073–2088.
13. Tomooka T., Shoji Y., Matsui T. High temperature vapor pressure of Si. Journal of the Mass Spectrometry of Japan. 1999;47(1):49–53. https://doi.org/10.5702/ massspec.47.49
14. Гиршфельдер Дж., Кертисс Ч., Берд Р. Молекулярная теория газов и жидкостей. М.: Изд-во иностр. лит-ры, 1961. 929 с.
15. Ageeva M.V., Demin V.A. Physical model and numerical simulation of high-temperature silicification of carbon composite material. Philosophical Transactions of the Royal Society A. 2023;381:20220083. https://doi.org/10.1098/rsta.2022.0083
16. Matsumoto M. Molecular dynamics simulation of interphase transport at liquid surfaces. Fluid Phase Equilibria. 1996;(125):195–203.
17. Matsumoto M. Molecular dynamics of fluid phase change. Fluid Phase Equilibria. 1998;(144):307–314.
18. Bond M., Struchtrup H. Mean evaporation and condensation coefficients based on energy dependent condensation probability. Physical Review E 70. 2004;061605. https://doi.org/10.1103/PhysRevE.70.061605
19. Schwabl Fr. Statistical mechanics. Berlin: Springer, 2006. 577 p.
20. Nield D.A., Bejan A. Convection in porous media. N.Y.: Springer, 2006. 654 p.
21. Демин В.А., Петухов М.И., Пономарев Р.С., Топова А.В. О роли анизотропии и нелинейных диффузионных эффектов при формировании волноводов в кристалле ниобата лития. Вестник Пермского университета. Физика. 2021;(1):49–58. https://doi.org/10.17072/1994-3598-2021-1-49-58
22. Vohra S.T., Mickelson A.R., Asher S.E. Diffusion characteristics and waveguiding properties of proton exchanged and annealed LiNbO3 channel waveguides. Journal of Applied Physics (AIP). 1989;66(11):5161–5174. https://doi.org/10.1063/1.343751
23. Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. М.: Наука, 1984. 831 с.
24. Самарский А.А. Теория разностных схем. М.: Наука, 1989. 616 с.
Об авторах
М. В. АгееваРоссия
Мария Викторовна Агеева – инженер-исследователь лаборатории подземной утилизации углерода Института механики сплошных сред (ИМСС) УрО РАН; магистр Пермского государственного национального исследовательского университета (ПГНИУ)
Россия, 614068, г. Пермь, ул. Букирева, 15
Россия, 614013, г. Пермь, ул. Королева, 1
В. А. Демин
Россия
Виталий Анатольевич Демин – д.ф.-м.н., профессор, заведующий кафедрой теоретической физики ПГНИУ; профессор кафедры общей физики Пермского национального исследовательского политехнического университета
Россия, 614068, г. Пермь, ул. Букирева, 15
Россия, 614990, г. Пермь, Комсомольский пр-т, 29
Т. В. Демина
Россия
Татьяна Витальевна Демина – инженер-исследователь лаборатории подземной утилизации углерода ИМСС УрО РАН; аспирант кафедры теоретической физики ПГНИУ
Россия, 614068, г. Пермь, ул. Букирева, 15
Россия, 614013, г. Пермь, ул. Королева, 1
Рецензия
Для цитирования:
Агеева М.В., Демин В.А., Демина Т.В. Физико-математическая модель доставки паров кремния в ходе высокотемпературного силицирования пористых углеродных материалов. Известия вузов. Порошковая металлургия и функциональные покрытия. 2024;18(3):49-61. https://doi.org/10.17073/1997-308X-2024-3-49-61
For citation:
Ageeva M.V., Demin V.A., Demina T.V. Physical and mathematical model of the silicon vapor transport during high-temperature silicification of a porous carbon media. Powder Metallurgy аnd Functional Coatings (Izvestiya Vuzov. Poroshkovaya Metallurgiya i Funktsional'nye Pokrytiya). 2024;18(3):49-61. https://doi.org/10.17073/1997-308X-2024-3-49-61
JATS XML